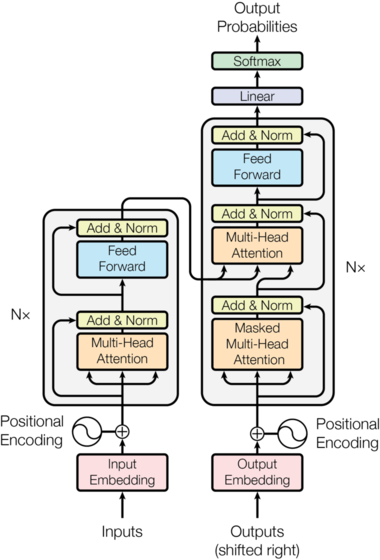
Machine Learning involves teaching computers to learn from data. Understanding the mathematical foundations behind ML is crucial for grasping how algorithms work and how to apply them effectively. We will discuss the essential mathematical concepts, including linear algebra, probability, statistics, calculus, and data structures.
Linear Algebra Basics
Linear algebra is the branch of mathematics that deals with vectors and matrices. It plays a critical role in ML, as many algorithms rely on these structures.
Key Concepts:
- Vectors: A vector is an ordered list of numbers. It can represent data points in space. For example, a point in a 3D space can be represented as a vector \( \mathbf{v} = [x, y, z] \) .
- Matrices: A matrix is a rectangular array of numbers, arranged in rows and columns. It can represent multiple vectors. For instance, a matrix can hold several data points, where each row represents a different point, and each column represents a different attribute.
- Matrix Operations:
- Addition: Adding two matrices of the same size involves adding corresponding elements.
- Scalar Multiplication: Multiplying a matrix by a number (scalar) scales each element.
- Matrix Multiplication: This involves a more complex operation where rows from the first matrix multiply with columns from the second matrix.
- Linear Transformations: These are functions that map vectors to other vectors, often represented by matrices. Understanding how transformations work is essential for grasping how ML models manipulate data.
Probability and Statistics
Probability and statistics are vital for making informed predictions and decisions based on data. They help in understanding uncertainty and variability.
Distributions
Distributions describe how values of a random variable are spread or concentrated. Understanding these can help us make sense of data.
- Normal Distribution: Also known as the Gaussian distribution, it’s a bell-shaped curve that represents data clustering around the mean (average). Many ML algorithms assume that data follows a normal distribution.
- Binomial Distribution: This distribution represents the number of successes in a fixed number of trials, assuming each trial has two possible outcomes (success / failure).
- Uniform Distribution: In this distribution, all outcomes are equally likely; for example, rolling a fair die.
Bayes’ Theorem
Bayes’ Theorem is a fundamental concept in probability that explains how to update the probability of a hypothesis based on new evidence.
- Formula:
\[
P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}
\] - P(A|B): Probability of hypothesis A given data B.
- P(B|A): Probability of observing data B given that A is true.
- P(A): Prior probability of A.
- P(B): Total probability of B.
- Applications in ML: Bayes’ Theorem is used in various algorithms, including Naive Bayes classifiers, which are popular for spam detection and text classification tasks.
Calculus and Optimization
Calculus is the mathematical study of change. It allows us to model and understand changes in data. Optimization is about finding the best solution among many possibilities.
Key Concepts in Calculus:
- Derivatives: A derivative measures how a function changes as its input changes. In ML, derivatives help us determine the slope of a function and are essential for optimization.
- Gradient: The gradient is a vector that contains all the partial derivatives of a function. It points in the direction of the greatest rate of increase. We often use gradients in ML for adjusting parameters in algorithms.
Optimization:
- The goal of optimization in ML is to minimize or maximize a function (typically a cost or loss function).
- Methods:
- Gradient Descent: An iterative method for finding the minimum of a function. It involves taking steps proportional to the negative of the gradient.
- Learning Rate: This is a hyperparameter that controls how much we adjust the parameter values with respect to the loss gradient. A small learning rate can lead to slow convergence, while a large rate can overshoot the minimum.
Data Structures and Algorithms
Data structures and algorithms are essential for efficiently processing and storing data. They decide how we manipulate data and implement ML algorithms.
Key Data Structures:
- Arrays: A collection of elements identified by index; they are used to store data of the same type.
- Lists: Similar to arrays, but they can hold elements of various types and can dynamically change in size.
- Dictionaries: A collection of key-value pairs. They allow for fast data retrieval based on a unique key.
Important Algorithms in ML:
- Sorting: Sorting algorithms (like quicksort and mergesort) organize data, making it easier to analyze.
- Search Algorithms: These algorithms find specific data points within a structure. For example, binary search efficiently finds an item from a sorted list.
- Classification Algorithms: Such as decision trees and support vector machines, these algorithms categorize data into classes based on patterns learned from training data.
Understanding these mathematical foundations is essential for delving deeper into machine learning. They equip you with the fundamental tools you need to grasp more complex concepts and algorithms in this exciting field. As you continue your journey in ML, revisiting these principles will be invaluable as you tackle real-world data problems.
Subscribe to our newsletter!