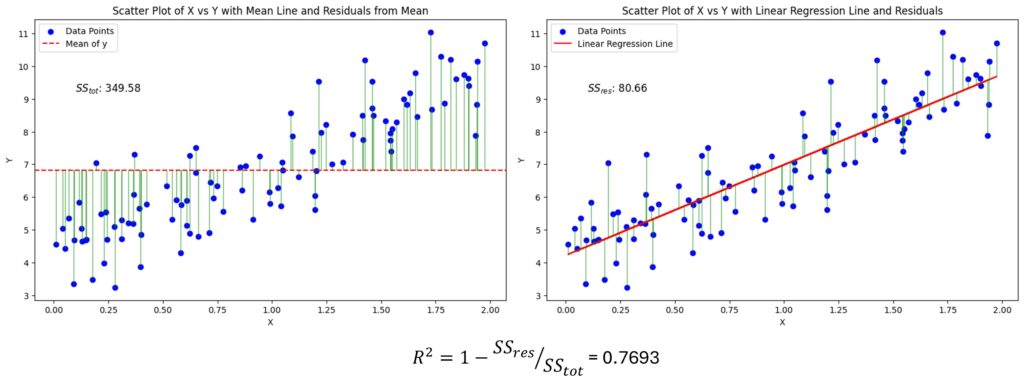
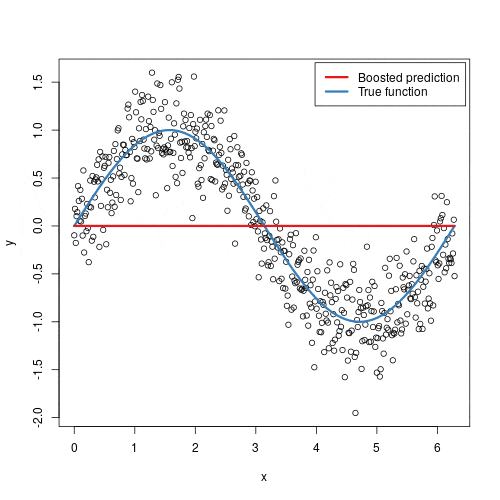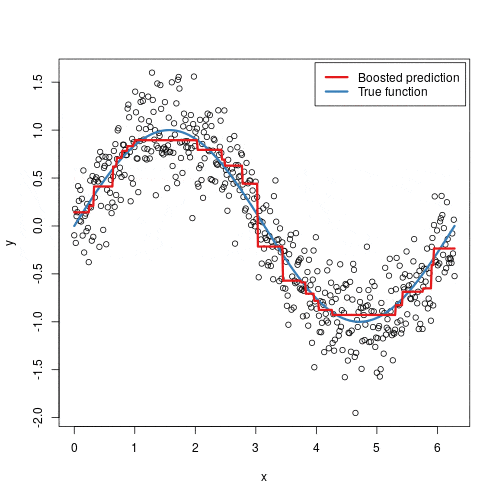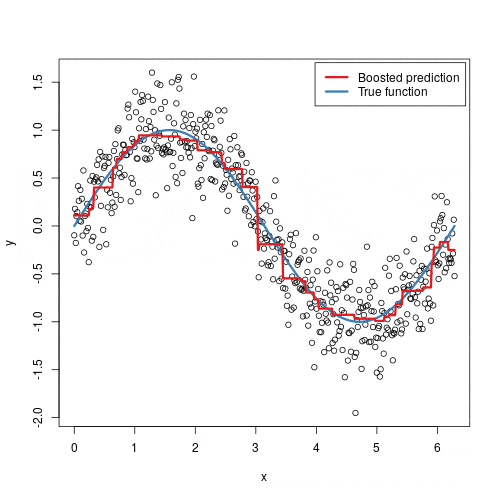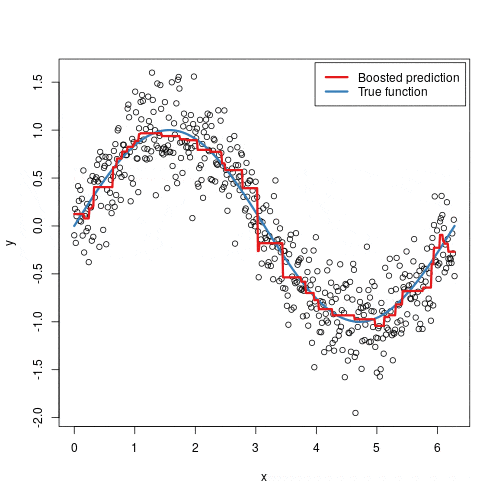
Random forest is a powerful ensemble learning algorithm used for both classification and regression tasks. It operates by constructing multiple decision trees during training and outputting the mode of the classes (classification) or mean prediction (regression) of the individual trees. This method helps to improve predictive accuracy and control overfitting.
Part 1: Foundations of Ensemble Learning & Decision Trees

1.1 The Wisdom of the Crowd: Core Concept
Ensemble learning mimics the idea that aggregating multiple (imperfect, diverse) opinions produces a more reliable answer than relying on a single source. Individual models (often called “base learners” or “weak learners”) make errors in different places; if their errors are uncorrelated (or at least not perfectly correlated), aggregation reduces variance and improves generalization.
Combining the predictions of multiple weak learners can lead to a single, more accurate, and robust model (a “strong learner”). This is analogous to the “wisdom of the crowd” phenomenon, where the collective opinion of a diverse group of individuals is often better than that of a single expert. By aggregating the “votes” of many models, we can average out their individual errors.
Key intuition:
- Single tree: low bias? (if deep) but high variance.
- Many diversified trees + averaging/voting: variance drops roughly proportional to
ρ * σ²whereρis average correlation among trees. Reducing correlation is as important as reducing individual variance.
How does Random Forest use bagging?
- Random Forest creates many decision trees, each trained on a unique “bootstrap” sample: a random subset of the training data, sampled with replacement.
- Each tree learns patterns from its own sample, so their mistakes are less likely to overlap.
- When making predictions, Random Forest aggregates the outputs of all trees—by majority vote for classification or averaging for regression—yielding a more stable and accurate result.
Why does this work?
- Individual deep decision trees are powerful but prone to overfitting (high variance).
- By averaging many such trees, Random Forest dramatically reduces variance while keeping bias low.
- The randomness in both data sampling and feature selection at each split ensures the trees are diverse, further improving generalization.
Technical summary:
Random Forest = Bagging (bootstrap sampling) + Random feature selection per split + Unpruned decision trees + Aggregation (voting/averaging).
This synergy makes Random Forest a robust, intuitive, and practical ensemble method for a wide range of machine learning tasks.
1.2 Decision Trees: The Building Blocks
A decision tree is a flowchart-like structure where:
- Root Node: The topmost node, representing the entire dataset.
- Internal Nodes: Represent a test on a feature. Split on feature thresholds (numerical) or partitions (categorical).
- Branches: Represent the outcome of the test.
- Leaf Nodes (or Terminal Nodes): Represent a class label (in classification) or a continuous value (in regression).
At each node, the tree selects the feature and threshold that best separates the data according to a criterion (e.g., Gini impurity for classification, mean squared error for regression). The process repeats recursively, growing branches until a stopping condition is met (pure leaf, minimum samples, or maximum depth).
Overfitting in Decision Trees
- Deep/unpruned trees memorize noise: near-zero training error, overfitting, poor generalization.
- Indicators: huge number of leaves, leaves with 1–2 samples, unstable splits under small data perturbations.
Random Forest typically grows unpruned trees (low bias) and handles overfitting via aggregation.
1.3 Bias-Variance Tradeoff
In machine learning, a model’s prediction error can be decomposed into three parts: bias, variance, and irreducible error.
- Bias: The error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting).
- Variance: The error from sensitivity to small fluctuations in the training set. High variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs (overfitting).
The bias-variance tradeoff is the conflict in trying to simultaneously minimize these two sources of error. Ensemble methods are effective because they can reduce variance (like in bagging) or bias (like in boosting) without a significant increase in the other component.
- Generalization error ≈ Bias² + Variance + Irreducible noise. (check here)
- Deep trees: low bias, high variance.
- Shallow trees: higher bias, lower variance.
- Random Forest (RF) keeps trees deep (low bias) while mitigating variance via bagging + feature subsampling to decorrelate trees.
- RF rarely reduces bias relative to a single deep tree; its strength is variance reduction without much bias penalty.
Part 2: The Random Forest Algorithm
2.1 Core Mechanics of Random Forest
2.1.1 Bootstrap Aggregating (Bagging) in Action
Random Forest builds upon the idea of bagging. It creates multiple bootstrap samples from the training data (random samples with replacement). For each bootstrap sample, a separate decision tree is trained. Because each tree sees a slightly different subset of the data, they each become unique “experts.”
For each tree: draw a bootstrap sample of size max_samples from training set of size N (sampling with replacement).
If we consider max_samples exactly equal to N, then each tree is trained on about 63% (why? check FAQ) of the total training data due to bootstrapping. The remaining one-third, not used in training that specific tree, are called “out-of-bag” (OOB) samples.
2.1.2 Feature Randomness (Random Subspace Method)
This is the key innovation of Random Forest over simple bagging of decision trees. When splitting a node, a random forest does not consider all features. Instead, it selects a random subset of features and only considers those for the split. This “feature randomness” decorrelates the trees. If one feature is very predictive, bagging would result in many trees using this feature for their top splits, making them highly correlated. By restricting the choice of features, other features get a chance to contribute, leading to a more diverse and robust ensemble.
At each split, instead of considering all features d, consider a random subset of size max_features (max_features << d). This reduces correlation between trees. Typical defaults:
- Classification:
max_features = sqrt(d) - Regression:
max_features = d / 3(heuristic)
Tuning max_features controls bias–variance–correlation tradeoffs.
2.1.2 Algorithm Construction: A Step-by-Step Guide
- For t = 1..
n_estimators:- Sample
max_samplestraining instances with replacement → bootstrap set \(D_t\). - Grow an unpruned tree:
- At each node, randomly select
max_featuresfeatures. - Find the best split using chosen impurity or MSE criterion.
- Repeat until stopping rule (often pure or
min_samples_leaf/min_samples_splitconstraints) is met.
- Sample
- Store tree \(T_t\).
- Prediction:
- Classification: majority vote of \({T_t(x)}\).
- Regression: average of \({T_t(x)}\).
2.2 Computational cost
Training Complexity: \(O(\text{n_estimators} \cdot \text{max_features} \cdot N \log^2 N)\)
For a single decision tree:
n_estimators: the number of trees in the forest. Training is directly proportional to the number of trees.- At each split, we consider
max_featuresfeatures. - The \(O(N \log N)\) term comes from the process of sorting the features to find the best split points for each node in a decision tree, but with efficient implementations (e.g., presorting or histograms), this can be reduced.
- If tree has depth \(d\), the total cost of building the tree is roughly \(O(\text{max_features} \cdot N \log N \cdot d)\). But in practice trees stop when leaves are pure or too small. The average depth is \(O(\log N)\) for balanced trees.
So, training one tree is about: \(O(\text{max_features} \cdot N \log^2 N)\)
For a forest with \(\text{n_estimators}\) trees: \(O(\text{n_estimators} \cdot \text{max_features} \cdot N \log^2 N)\)
(Bootstrap sampling adds \(O(\text{max_samples})\) per tree, negligible compared to splits.)
Prediction Complexity: \(O(\text{n_estimators} \cdot \log N)\)
To predict with one tree: traverse from root to leaf. Depth is \(O(\log N)\) (balanced) or up to \(O(N)\) (worst case).
So for \(\text{n_estimators}\) trees: \(O(\text{n_estimators} \cdot \log N)\)
2.3 Prediction Process
Classification: [Majority Voting] Each tree outputs a class label (or class probability distribution). Soft voting (averaging probabilities) often yields smoother decision boundaries than hard majority.
Regression: [Averaging Predictions] Mean reduces variance. Median (not standard in classic RF) can be more robust to outlier trees; sometimes we need quantile regression forests to estimate conditional distributions.
2.4 Key Hyperparameters and Their Impact
2.4.1 Tree-Specific Parameters
max_depth: The maximum depth of the tree. Deeper trees can model more complex relationships but are more prone to overfitting. Lowermax_depthresults in higher bias, lower variance, and faster training.min_samples_split: Minimum samples required to attempt a split. Higher values prevent very granular partitions → regularization.min_samples_leaf: Minimum samples per leaf. Strong control against overfitting and smoothing predictions. For imbalanced classification, set >1 to prevent rare-class dominated micro-leaves.max_leaf_nodes: Cap number of terminal nodes; implicitly balances depth/branching; useful for bounding model size.
2.4.2 Forest-Specific Parameters
n_estimators: The number of trees in the forest. More trees generally improve performance and make predictions more stable. Error typically plateaus; beyond that only increases training + inference time. Largern_estimatorsreduces variance ~ 1/n_estimatorswhen trees weakly correlated.max_features: Number (or fraction) of features considered at each split. A smallermax_featuresreduces the correlation between trees, generally reducing variance but potentially increasing bias. Too smallmax_featurescan underfit.bootstrap: If True (default), use sampling with replacement. If False, each tree sees the whole dataset (less variance reduction; OOB unavailable). Subsampling without replacement + feature randomness can mimic Extremely Randomized Trees (Extra-Trees) which often use random split thresholds too.oob_score: If True, computes OOB accuracy using aggregated predictions from trees not trained on each sample. Offers internal validation without a separate holdout.
Additional commonly encountered knobs:
class_weight: For imbalance handling by adjusting impurity weighting.n_jobs: Parallelism.
Tuning heuristics:
- Start with default depth (unbounded) + moderate
n_estimators(e.g., 200) + OOB enabled. - Adjust
max_featuresto see bias–variance shifts. - Regularize with
min_samples_leafbefore constraining depth. - Increase
n_estimatorsuntil OOB / validation curve flattens.
Part 3: Model Evaluation and Interpretation
3.1 Performance Metrics
3.1.1 Out-of-Bag (OOB) Error Estimation
For each sample i, collect predictions from trees where i was not included in the bootstrap. Aggregate for classification (vote) or regression (mean). This provides an approximately unbiased estimate of generalization when dataset is sufficiently large and representative. Caveats: Slight optimistic bias with heavy tuning on OOB itself; higher variance for small N.
3.1.2 Cross-Validation with Random Forest
Still valuable when:
- You need more stable estimates than OOB (especially small or high-variance tasks).
- Comparing RF against other algorithm families under identical splits.
Use stratified k-fold for classification; and repeated CV for robustness.
3.2 Understanding Model Insights
3.2.1 Feature Importance
Random Forest provides an estimate of the importance of each feature.
Mean Decrease in Impurity (MDI / Gini Importance): This is calculated as the total reduction in the criterion (Gini impurity or MSE) brought by a feature, averaged over all trees in the forest. It is fast to compute but can be biased towards high-cardinality / continuous features. This is the default method used in many implementations like sklearn.ensemble.RandomForestClassifier and RandomForestRegressor.
$
\text{Feature Importance}(f_j) = \frac{1}{T} \sum_{t=1}^{T} \sum_{\text{splits on } f_j} \text{(impurity decrease)} \times \frac{\text{samples at node}}{\text{total samples}}
$
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier()
rf.fit(X, y)
importances = rf.feature_importances_Permutation Importance: This is a more reliable method. The importance of a feature is measured by calculating the increase in the model’s prediction error after permuting the feature’s values. A feature is “important” if shuffling its values increases the model error, because it means the model relied on that feature for making predictions. Pros: Model-agnostic. Cons: Correlated features can mask each other (conditional vs marginal importance issue). Use grouped permutation or conditional permutation variants for correlated blocks.
Steps:
- Measure baseline accuracy (or MSE) on a validation set.
- For each feature:
- Shuffle its values (breaking its relationship with the target).
- Recalculate performance.
- The drop in performance indicates the feature’s importance.
from sklearn.inspection import permutation_importance
result = permutation_importance(rf, X_test, y_test, n_repeats=10, random_state=42)
importances = result.importances_meanMean Decrease in Accuracy (MDA)
A variant of permutation importance often used in out-of-bag (OOB) settings within Random Forests:
- For each tree, measure OOB accuracy.
- Randomly permute one feature and measure new OOB accuracy.
- Importance = decrease in accuracy.
| Method | Core Idea | Pros | Cons | Bias Risk |
|---|---|---|---|---|
| Impurity-based (MDI) | Avg. impurity decrease per feature | Fast, built-in | Biased toward features with many categories or continuous values; Can give misleading results if features are correlated | High |
| Permutation-based | Drop in performance when shuffled | Model-agnostic, intuitive | Slower; Can be affected by correlation(shuffling one correlated feature might not drop accuracy much) | Moderate |
| MDA (OOB) | Permutation on OOB data | Efficient for RF | Needs OOB setup | Moderate |
3.2.2 Model Interpretability Techniques
- Visualizing a Single Tree from the Forest: Select a representative tree (e.g., median depth). Use for educational insight only; not a faithful global explanation because forest prediction aggregates many diverse trees.
- Partial Dependence Plots (PDP): PDPs show the marginal effect of a feature on the predicted outcome of a machine learning model. It can show whether the relationship between the target and a feature is linear, monotonic, or more complex. For a feature $X_j$, PDP is computed by averaging the model’s predictions over the distribution of all other features while varying $X_j$.
- Pros: Simple, intuitive global view.
- Cons: Assumes feature independence; can mislead if features correlated. Averages can hide heterogeneous effects. Use with caution; consider joint PDPs for interacting features.
- Individual Conditional Expectation (ICE) Plots: ICE plots are a more granular version of PDPs. They display one line per instance, showing how that instance’s prediction changes when a feature is varied. This can reveal heterogeneous relationships that are masked by the average PDP.
- Pros: Reveals individual-level effects; useful for spotting interactions and non-linearities.
- Cons: Can be noisy; harder to interpret with many instances. Consider centering (c-ICE) to highlight differences.
- SHAP (SHapley Additive exPlanations) Values: SHAP is a game-theoretic approach to explain the output of any machine learning model. It connects optimal credit allocation with local explanations using the classic Shapley values from game theory. For a given prediction, SHAP values compute the contribution of each feature to the prediction, providing a powerful way to understand why a specific decision was made.
- Pros: Consistent, locally accurate, handles feature interactions. Provides both global (summary plots) and local (force plots) interpretability.
- Cons: Computationally intensive for large datasets/models; approximations may be needed. Interpretation requires care, especially with correlated features.
Interpretation strategy:
- Start with permutation importance to prioritize features impacting performance.
- Use SHAP summary for global distribution + interaction hints.
- Drill down with PDP/ICE for top features to understand monotonicity / thresholds.
- Sanity-check with domain knowledge; validate stability across resamples.
Part 4: Practical Aspects and Advanced Topics
4.1 Implementation Aspects
4.1.1 Data Preprocessing (Categorical + Numerical)
One of the appealing features of the Random Forest algorithm is its flexibility with different data types.
- Numerical Data: Random Forest handles numerical features naturally without requiring feature scaling (like standardization or normalization). The tree-based structure is insensitive to the scale of the features because it only cares about the order of values for finding split points.
- Categorical Data: How categorical data is handled depends on the specific library implementation. The popular
scikit-learnimplementation requires categorical features to be converted into a numerical format, typically through one-hot encoding or ordinal encoding. However, one-hot encoding can lead to high-dimensional data if the categorical feature has many levels, which may impact performance and interpretability. So, consider:- Low/medium cardinality: One-hot encoding is usually fine.
- High cardinality: Consider target (mean) encoding with proper cross-validation to avoid leakage, hashing tricks, or grouping rare categories into an “Other” category.
- Text Data: For text features, it’s common to use techniques like TF-IDF (Term Frequency-Inverse Document Frequency) or word embeddings (like Word2Vec or BERT) to convert text into numerical vectors. These representations can then be fed into the Random Forest model.
- Time Series Data: For time series features, you might need to create lagged features or rolling statistics (like moving averages) to capture temporal patterns before feeding them into the model.
- Mixed Data Types: If your dataset contains a mix of different data types (e.g., numerical, categorical, text), you’ll need to preprocess each type appropriately before combining them into a single feature matrix.
Missing Values: Random Forest can handle missing values in features to some extent, but it’s generally a good practice to impute missing values before training. Simple imputation methods like using the median for numerical features and the most frequent category for categorical features often work well.
4.1.2 Handling Imbalanced Datasets
When dealing with imbalanced classes, standard Random Forest can be biased. Common strategies to address this include:
class_weightparameter: Inscikit-learn, settingclass_weight='balanced'automatically adjusts weights inversely proportional to class frequencies.- Sampling Techniques: Using methods like SMOTE (Synthetic Minority Over-sampling Technique) to oversample the minority class or RandomUnderSampler to undersample the majority class before training the model.
4.1.3 Hyperparameter Tuning Strategies
Goal: shift along bias–variance–correlation surface efficiently.
Key knobs:
- Structural:
max_depth,min_samples_leaf,min_samples_split - Diversity:
max_features,bootstrap - Ensemble size:
n_estimators(grow until OOB / validation stabilizes) - Regularization via leaf size often smoother than capping depth early.
Approaches:
- Manual + OOB curve for quick baseline.
- Grid Search (
GridSearchCV): Exhaustively tries every combination of hyperparameters from a predefined grid. It is thorough but can be computationally very expensive. - Randomized Search (
RandomizedSearchCV): Samples a fixed number of hyperparameter settings from specified distributions. It is much more efficient than Grid Search and often finds a very good combination of parameters. - Bayesian Optimization: A more advanced technique (found in libraries like
OptunaorHyperopt) that uses the results from previous trials to inform which set of hyperparameters to try next. It intelligently navigates the search space to find the optimal parameters more quickly.
4.1.4 Implementation with Scikit-Learn (RandomForestClassifier, RandomForestRegressor)
Scikit-learn provides a straightforward and powerful implementation of Random Forest.
Here’s a basic example of using RandomForestClassifier:
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
# Generate synthetic data
X, y = make_classification(n_samples=1000, n_features=20, n_informative=10,
n_redundant=5, n_classes=2, random_state=42)
# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Initialize the Random Forest Classifier
# n_estimators: The number of trees in the forest.
# random_state: Ensures reproducibility.
rf_clf = RandomForestClassifier(n_estimators=100, random_state=42, oob_score=True)
# Train the model
rf_clf.fit(X_train, y_train)
# Make predictions
predictions = rf_clf.predict(X_test)
# Evaluate the model
accuracy = rf_clf.score(X_test, y_test)
print(f"Model Accuracy: {accuracy:.4f}")
# Check the Out-of-Bag score
print(f"OOB Score: {rf_clf.oob_score_:.4f}")The process for regression is nearly identical, simply using RandomForestRegressor and an appropriate regression metric for evaluation.
4.2 Comparison with Other Algorithms
4.2.1 Versus Single Decision Tree
- Tree: fast, interpretable, high variance
- RF: averages many deep trees to suppress variance, losing simple path interpretability but gaining accuracy
- A single tree is very prone to overfitting, whereas a Random Forest is robust against it.
4.2.2 Versus Gradient Boosting (XGBoost / LightGBM)
- Boosting often yields superior leaderboard accuracy on structured data
- RF trains fully in parallel and independently; boosting is sequential
- RF less sensitive to hyperparameters; boosting requires learning rate, depth, regularization tuning
- Boosting can reduce bias more aggressively; RF mainly attacks variance
- LightGBM handles very large, sparse, high-card data more efficiently
4.2.3 Versus SVM
- SVM (RBF): powerful in medium-dimensional dense spaces; needs scaling
- RF handles categorical + missing with simpler preprocessing
- SVM can struggle with very large N without approximate methods
- RF provides intrinsic (approximate) feature importance
- RF is a go-to for tabular data. SVMs can be very effective in high-dimensional spaces (e.g., text classification) and when a clear margin of separation exists between classes.
4.3 Variations and Extensions
4.3.1 Extremely Randomized Trees (ExtraTrees)
Idea: In addition to selecting a random subset of features at each node, it also selects the split point for each feature randomly, rather than finding the optimal split point.
Differences:
- Uses full dataset (often no bootstrap by default)
- Random split thresholds per candidate feature (drawn before evaluation)
Effect:
- Increases randomness; reduces variance further
- Sometimes slightly higher bias
- Often faster (no exhaustive threshold search)
Use when: speed and additional decorrelation help; try both RF & ExtraTrees in model selection.
4.3.2 Isolation Forest (Anomaly Detection)
Idea: Adaptation of RF principle for unsupervised anomaly detection. It works by building an ensemble of “Isolation Trees.” In these trees, features and split points are selected randomly to explicitly isolate observations. The logic is that anomalies are “few and different,” so they should be easier to isolate and will have a much shorter average path from the root to a leaf node.
Mechanics:
- Build many very random trees on subsamples
- Score = normalized inverse path length
Contrast: not optimizing impurity; objective is isolation efficiency, not predictive accuracy.
Part 5: Tools and Libraries
- Scikit-Learn:
RandomForestClassifierandRandomForestRegressorare robust, easy to use, and feature-rich. - H2O.ai: An open-source platform designed for scalable, distributed machine learning. Its Random Forest implementation is highly optimized for performance on large datasets.
- Spark MLlib: Apache Spark’s machine learning library, built for big data processing on distributed clusters. It provides a Random Forest implementation that can train on massive datasets.
- TensorFlow Decision Forests: A library that brings Random Forest and other tree-based models to the TensorFlow ecosystem, allowing for seamless integration with other TensorFlow tools.
FAQ
Why are about 63.2% of training samples used in each bootstrap sample when max_samples = N?
The 63.2% arises from the probability that a training example appears at least once in a bootstrap sample of size N drawn with replacement from N distinct records.
- For any specific example, the chance it is not picked in a single draw is (1 − 1/N).
- After N independent draws, the probability it is never selected is (1 − 1/N)^N, which tends to e^(−1) ≈ 0.3679 as N grows.
- Take natural logs. ln[(1 − 1/N)^N] = N · ln(1 − 1/N).
- Use Taylor expansion ln(1 − x) ≈ −x − x²/2 − …: N · ln(1 − 1/N) ≈ N · (−1/N − 1/(2N²) + …) = −1 − 1/(2N) + … → −1 as N → ∞.
- Exponentiating: (1 − 1/N)^N → e^(−1) ≈ 0.367879.
- Rounding: Often informally cited as “≈ 0.36” (coarse) or more precisely 0.368.
- Thus the complement—being selected at least once—is 1 − e^(−1) ≈ 0.6321, or about 63.2%. These are the “in-bag” (IB) instances for that tree.
The remaining ≈36.8% are “out-of-bag” (OOB) for that specific tree—meaning the tree never saw them during training. Because each tree has its own OOB subset, you can aggregate predictions for each training point from only the trees for which it was OOB, yielding an internal, nearly unbiased estimate of generalization error without a separate validation set. Each example is OOB for roughly 36.8% of the trees, providing enough votes to form a reliable OOB prediction when the forest is sufficiently large.
Why not use all features at each split?
Using all features at each split would lead to highly correlated trees, especially if some features are very predictive. This correlation reduces the variance reduction benefit of bagging. By randomly selecting a subset of features at each split, Random Forests promote diversity among the trees, which enhances the ensemble’s overall performance and robustness.
Why use unpruned trees in Random Forest?
Using unpruned trees allows each individual tree to capture complex patterns in the data, resulting in low bias. While unpruned trees are prone to overfitting when used alone, the ensemble approach of Random Forest mitigates this by averaging the predictions of many such trees. The randomness introduced through bootstrapping and feature selection helps to decorrelate the trees, which significantly reduces variance. This combination of low bias from deep trees and reduced variance from aggregation leads to a strong overall model.
Why use bootstrap sampling?
Bootstrap sampling (sampling with replacement) introduces variability in the training data for each tree, which helps to create diverse trees. This diversity is crucial for the effectiveness of ensemble methods like Random Forest, as it reduces the correlation between individual trees. Additionally, bootstrap sampling allows for the use of out-of-bag samples for internal validation, providing an unbiased estimate of model performance without needing a separate validation set.
How does Random Forest handle missing data?
Random Forest can handle missing data in several ways:
- Surrogate Splits: When a feature is missing for a particular instance, Random Forest can use surrogate splits—alternative features that are correlated with the primary splitting feature—to make decisions.
- Imputation: Missing values can be imputed using various strategies (e.g., mean, median, mode) before training.
- Tree Structure: The tree structure itself can accommodate missing values by allowing branches to be created for instances with and without the missing feature.
- Weighted Voting: During the aggregation of predictions, trees that do not have missing values for a particular instance can be given more weight.
Can Random Forest be used for multi-class classification?
Yes, Random Forest can be used for multi-class classification tasks. In this case, each tree in the forest outputs a class label, and the final prediction is typically made by majority voting among the trees. Random Forest naturally handles multi-class problems without any modifications to the underlying algorithm.
Can Random Forest classify multi-label data?
Yes, Random Forest can be adapted for multi-label classification tasks. In multi-label classification, each instance can belong to multiple classes simultaneously. One common approach is to use a one-vs-rest (OvR) strategy, where a separate Random Forest model is trained for each label. Each model predicts the presence or absence of its corresponding label, and the final prediction for an instance is a combination of the outputs from all models. Some implementations also support multi-label classification directly.
How does Random Forest compare to Gradient Boosting?
Random Forest and Gradient Boosting are both powerful ensemble learning methods, but they have different approaches and characteristics:
- Random Forest: Uses bagging and feature randomness to create an ensemble of unpruned decision trees. It is generally more robust to overfitting and requires less hyperparameter tuning. It is faster to train and can handle large datasets well.
- Gradient Boosting: Builds trees sequentially, where each new tree attempts to correct the errors of the previous trees. It often achieves higher accuracy than Random Forest but is more sensitive to hyperparameters and can overfit if not properly regularized. It is typically slower to train due to its sequential nature.
Can Random Forest handle categorical features?
Yes, Random Forest can handle categorical features. In decision trees, categorical features can be split by creating branches for each category or by grouping categories based on their relationship with the target variable. Most implementations of Random Forest, including scikit-learn, can directly handle categorical features by treating them as numerical values or using one-hot encoding. However, care should be taken with high-cardinality categorical features, as they can lead to overfitting if not properly managed.
How to tune hyperparameters in Random Forest?
Tuning hyperparameters in Random Forest involves adjusting several key parameters to optimize model performance. Here are some common hyperparameters to tune and strategies for doing so:
- n_estimators: The number of trees in the forest. Start with a moderate number (e.g., 100-200) and increase until performance plateaus.
- max_features: The number of features to consider when looking for the best split. Common choices are ‘sqrt’ for classification and ‘log2’ or a fraction of total features for regression. Experiment with different values to find the optimal balance between bias and variance.
- max_depth: The maximum depth of each tree. Deeper trees can capture more complex patterns but may overfit. Use cross-validation to find a depth that balances bias and variance.
- min_samples_split: The minimum number of samples required to split an internal node. Higher values prevent the model from learning overly specific patterns.
- min_samples_leaf: The minimum number of samples required to be at a leaf node. This parameter can help smooth the model and reduce overfitting.
- bootstrap: Whether to use bootstrap samples when building trees. Generally set to True for Random Forest.
What are the limitations of Random Forest?
While Random Forest is a powerful and versatile algorithm, it has several limitations:
- Interpretability: Random Forest models are often considered “black boxes” because it can be challenging to interpret the relationships between features and the target variable. While feature importance scores can provide some insights, understanding the exact decision-making process of the ensemble can be difficult.
- Memory Consumption: Random Forest can be memory-intensive, especially with a large number of trees and high-dimensional data. This can lead to increased training times and resource usage.
- Overfitting: Although Random Forest is generally robust to overfitting, it can still occur, particularly with noisy data or when the number of trees is excessively high. Proper tuning of hyperparameters is essential to mitigate this risk.
- Bias towards Dominant Classes: In imbalanced datasets, Random Forest may exhibit bias towards the majority class, leading to suboptimal performance on minority classes. Techniques such as class weighting or oversampling can help address this issue.
- Limited Extrapolation: Random Forest is primarily a regression and classification algorithm and may not perform well on tasks requiring extrapolation beyond the training data distribution.
- Sensitivity to Noisy Data: Random Forest can be sensitive to noisy data and outliers, which can affect the quality of the model. Preprocessing steps such as outlier removal and feature selection can help improve robustness.
How does Random Forest handle imbalanced datasets?
Random Forest can handle imbalanced datasets through several strategies:
- Class Weighting: Assigning different weights to classes can help the model pay more attention to minority classes. This can be done using the
class_weightparameter in scikit-learn. - Oversampling: Techniques like SMOTE (Synthetic Minority Over-sampling Technique) can be used to generate synthetic samples for the minority class, helping to balance the dataset.
- Undersampling: Reducing the number of samples from the majority class can also help balance the dataset, although this may lead to loss of information.
- Ensemble Techniques: Combining Random Forest with other techniques, such as boosting, can help improve performance on imbalanced datasets.
How to handle categorical features in Random Forest?
Random Forest can handle categorical features in several ways:
- Label Encoding: Categorical variables can be converted into numerical format using label encoding, where each category is assigned a unique integer. This is suitable for ordinal variables.
- One-Hot Encoding: For nominal variables, one-hot encoding can be used to create binary columns for each category. This approach is often preferred as it avoids introducing ordinal relationships between categories.
- Target Encoding: This technique involves replacing categorical values with the mean of the target variable for each category. While it can be effective, care must be taken to avoid data leakage.
- Using Tree-Based Methods: Random Forest and other tree-based algorithms can inherently handle categorical features without the need for extensive preprocessing. The algorithm can split on categorical variables directly.
- Handling High-Cardinality Features: For categorical features with many unique values, consider grouping rare categories into an “Other” category to reduce noise and improve model performance.
- Other encodings: Frequency encoding, binary encoding, hashing, and other strategies can also be explored based on the dataset and problem context.
How to visualize the top-k important features in Random Forest?
You can visualize the top-k important features in Random Forest using bar plots or horizontal bar charts. Here’s an example using Matplotlib and Seaborn in Python:
import matplotlib.pyplot as plt
import seaborn as sns
# Assuming 'rf' is your trained RandomForest model and 'feature_names' is a list of feature names
import numpy as np
# Get feature importances from the model
importances = rf.feature_importances_
# Get the indices of the top-k features
k = 10
top_k_indices = np.argsort(importances)[-k:]
# Plotting
plt.figure(figsize=(10, 6))
sns.barplot(x=importances[top_k_indices], y=np.array(feature_names)[top_k_indices])
plt.title(f"Top {k} Important Features")
plt.xlabel("Feature Importance")
plt.ylabel("Feature Names")
plt.show()How to get the median depth tree from a Random Forest?
To extract the median depth tree from a Random Forest, you can follow these steps:
import numpy as np
# Get the depths of all trees in the forest
depths = [tree.get_depth() for tree in rf.estimators_]
# Compute the median depth
median_depth = np.median(depths)
# Find the index of the tree with the median depth
median_tree_index = np.argsort(depths)[len(depths) // 2]
# Extract the median depth tree
median_tree = rf.estimators_[median_tree_index]References
- Breiman, L. (2001). Random Forests. Machine Learning, 45(1), 5-32. https://doi.org/10.1023/A:1010933404324
- Scikit-learn Random Forest Documentation
- Article on model complexity