ML Clustering: A Simple Guide

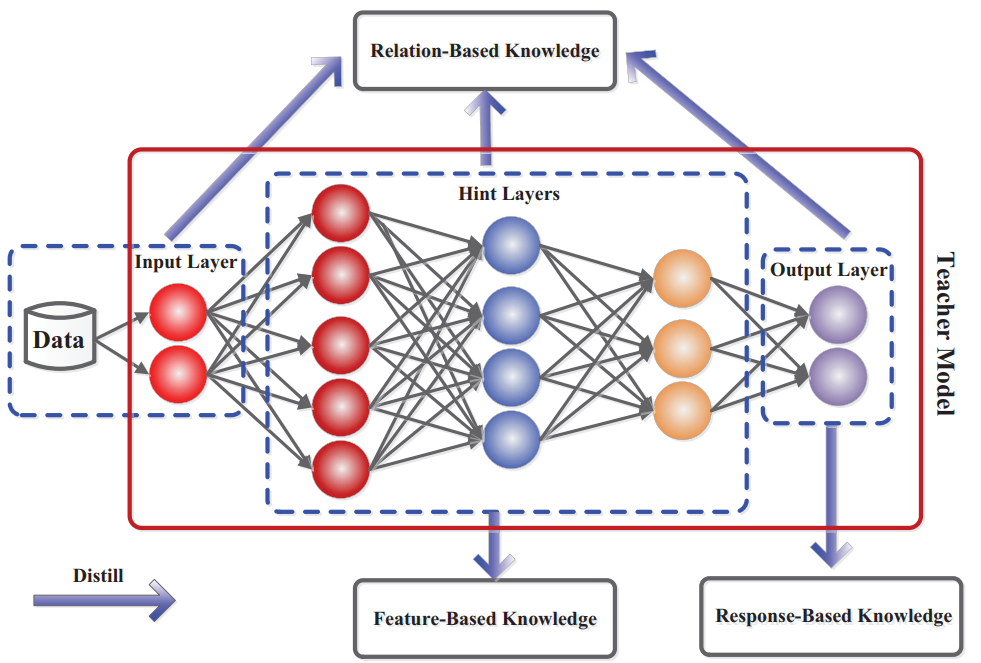
Clustering is an unsupervised ML that aims to categorize a set of objects into groups based on similarity. The core principle underlying clustering is that objects within the same cluster exhibit higher similarity to each other than to those in different clusters.

By grouping a set of objects into clusters based on their similarities, clustering aids in uncovering the inherent structure of data without pre-labeled instances.

Types of Clustering Techniques

Clustering techniques can be categorized into several types based on different criteria. The major categories include:

1. Partitioning Methods
2. Hierarchical Methods
3. Density-Based Methods
4. Grid-Based Methods
5. Model-Based Methods
6. Constraint-Based Methods

Q: What are the key “Distance Metrics” used for clustering?

Distance metrics define how similarity is computed between data points. Common metrics include:

• Euclidean Distance: This is the most commonly used distance metric, defined as the straight-line distance between two points in Euclidean space. For points \( p = (p_1, p_2, …, p_n) \) and \( q = (q_1, q_2, …, q_n) \), it is calculated as: \[
  d(p, q) = \sqrt{\sum_{i=1}^{n}(p_i – q_i)^2}
  \]
• Manhattan Distance: Also known as city block distance, this metric computes the distance as the sum of absolute differences: \[
  d(p, q) = \sum_{i=1}^{n} |p_i – q_i|
  \]
• Cosine Similarity: Widely used in text mining and information retrieval, it measures the cosine of the angle between two non-zero vectors. It is given by: \[
  \text{cosine}(A, B) = \frac{A \cdot B}{||A|| \cdot ||B||}
  \]
• Minkowski Distance: A generalization of both Euclidean and Manhattan distances, defined by a parameter \( p \): \[
  d(p, q) = \left(\sum_{i=1}^{n}|p_i – q_i|^p\right)^{1/p}
  \]

1. Partitioning Methods

Partitioning methods involve dividing a dataset into distinct clusters where each object belongs exclusively to one cluster. The most prominent technique in this category is the k-means algorithm.

K-Means Clustering

K-means clustering is an iterative algorithm that seeks to partition n observations into k clusters. The algorithm follows these steps:

1. Initialization: Select k initial cluster centroids (randomly or via a heuristic).
2. Assignment Step: Assign each data point to the nearest centroid based on a distance metric, typically Euclidean distance.
3. Update Step: Recalculate the centroids by taking the mean of all data points assigned to each cluster.
4. Convergence Check: Repeat the assignment and update steps until the centroids no longer change or a predefined number of iterations is reached.

The computational complexity of k-means is \(O(n * k * i)\), where n is the number of data points, k is the number of clusters, and i is the number of iterations. K-means is sensitive to the initial selection of centroids, which can lead to different cluster outputs. As a remedy, the k-means++ algorithm improves the initialization step by spreading the initial centroids.

Advantages and Limitations

Advantages:

• Computationally efficient for large datasets.
• Simple implementation.
• Works well with globular-shaped clusters.

Limitations:

• Requires the number of clusters (k) to be specified a priori.
• Sensitive to outliers and noise.
• Assumes spherical clusters and equal sizes.

2. Hierarchical Methods

Hierarchical clustering involves creating a hierarchy of clusters, either agglomeratively (bottom-up) or divisively (top-down). In agglomerative clustering, each data point starts in its own cluster, and pairs of clusters are merged iteratively based on a defined linkage criterion.

Agglomerative Clustering

The agglomerative clustering algorithm follows these steps:

1. Initialization: Assume each data point is a separate cluster.
2. Distance Computation: Compute the distance between all pairs of clusters.
3. Merging Step: Identify the pair of clusters with the smallest distance and merge them.
4. Update Distances: Recalculate the distances between the new cluster and the remaining clusters.
5. Repeat: Continue until a single cluster remains or until a desired number of clusters is formed.

Linkage Criteria: The critical part of hierarchical clustering lies in the choice of linkage criteria, which defines the distance between clusters. Common criteria include:

• Single Linkage: Distance based on the closest pair of points.
• Complete Linkage: Distance based on the farthest pair of points.
• Average Linkage: Average distance between all pairs.
• Ward’s Linkage: Minimizes the total within-cluster variance.

Advantages and Limitations

Advantages:

• Does not require a pre-specified number of clusters.
• Produces a dendrogram that visualizes the clustering process.
• Capable of identifying clusters of arbitrary shapes.

Limitations:

• High computational cost is \(O(n^3)\) for distance calculations.
• Sensitive to noise and outliers.

3. Density-Based Methods

Density-based clustering algorithms group together data points that are densely packed, marking distinct groups from those that lie in low-density regions. One of the most well-known density-based techniques is DBSCAN (Density-Based Spatial Clustering of Applications with Noise).

DBSCAN Clustering

DBSCAN clusters data based on two parameters:

• Epsilon (\( \epsilon \)): The maximum distance between two samples for them to be considered as in the same neighborhood.
• MinPts: The minimum number of points in a neighborhood for a point to be classified as a core point.

The algorithm operates as follows:

1. For each point in the dataset, determine its \( \epsilon \)-neighborhood.
2. If a point is a core point (i.e., it has at least MinPts in its \( \epsilon \)-neighborhood), form a cluster starting from this point.
3. Recursively include all reachable points from the core point until no more points can be added.
4. Classify any points that are not part of a cluster as outliers or noise.

Advantages and Limitations

Advantages:

• Can identify arbitrary-shaped clusters.
• Robust to noise and outliers.
• Does not require a predefined number of clusters.

Limitations:

• Performance is sensitive to the selection of \( \epsilon \) and MinPts.
• Struggles with clusters of varying density and high-dimensional datasets.

4. Grid-Based Methods

Grid-based clustering algorithms segment the data space into a finite number of cells, allowing for efficient cluster construction and retrieval. One exemplary algorithm in this category is STING (Statistical Information Grid).

STING Algorithm

The STING algorithm operates by:

1. Dividing the spatial area into multiple rectangular grid cells.
2. Sampling the data points in each grid cell and computing statistical characteristics such as mean, variance, and density.
3. Merging adjacent cells based on the statistical characteristics to form clusters.

STING utilizes a hierarchical cell structure, allowing for efficient access and merging.

Advantages and Limitations

Advantages:

• Fast processing owing to grid-based indexing.
• Can handle large datasets effectively.

Limitations:

• Requires a predefined grid size.
• Clusters may be influenced by the grid configuration, potentially leading to arbitrary results.

5. Model-Based Methods

Model-based clustering techniques assume a statistical model underlying the data distribution and aim to optimize the fit of the model to the data. One popular method is Gaussian Mixture Models (GMM).

Gaussian Mixture Models

GMM represents data as a mixture of several Gaussian distributions. The algorithm follows these steps:

1. Initialization: Define the number of components k and initialize parameters (mean, variance, and mixture weights).
2. Expectation Step (E-Step): Calculate the probability of each data point belonging to each Gaussian component.
3. Maximization Step (M-Step): Update the parameters of the Gaussian distributions based on the probabilities computed in the E-step.
4. Repeat the E and M steps until convergence.

The Expectation-Maximization algorithm underlies GMM, providing a robust approach to clustering that accounts for uncertainty in data assignment.

Advantages and Limitations

Advantages:

• Flexible in modeling clusters of different shapes and sizes.
• Provides a probabilistic approach, allowing for uncertainty quantification.

Limitations:

• Requires predefined k and sensitive to initialization.
• Complex and computationally expensive for large data.

6. Constraint-Based Methods

Constraint-based clustering methods incorporate user-defined constraints into the clustering process. These constraints can be either must-link (indicating that two points must belong to the same cluster) or cannot-link (indicating that two points must not belong to the same cluster).

Framework for Constraint-Based Clustering

The framework is generally as follows:

1. Constraint Definition: Define must-link and cannot-link constraints.
2. Clustering Algorithm: Use a chosen clustering algorithm (e.g., k-means or hierarchical) while incorporating the constraints.
3. Optimization: Optimize the clustering assignment subject to the constraints, often through iterative refinement.

Advantages and Limitations

Advantages:

• Allows users to influence clustering, leading to more desirable outputs.
• Useful in applications where domain knowledge is essential.

Limitations:

• The performance may be highly dependent on the quality of constraints.
• Computationally intensive when handling a large number of constraints.

Evaluation Metrics for Clustering

Evaluating clustering results is crucial as there is often no ground truth for unsupervised clustering. Several evaluation metrics fall into two broad categories: external and internal evaluation metrics.

1. External Evaluation Metrics

External metrics assess clustering quality against a known ground truth. Key external metrics include:

• Rand Index (RI): Measures the percentage of pairs that are correctly classified. The Rand Index ranges from 0 to 1, where 1 indicates perfect agreement.

\[
RI = \frac{\text{(number of agreeing pairs)}}{\text{(total number of pairs)}} =\frac {a+b}{n \choose 2} = \frac {a+b}{\frac{n(n-1)}{2}}
\]
where \(a\) is the number of pairs that are in the same cluster in both the true and predicted clusterings, and \(b\) is the number of pairs that are in different clusters in both clusterings.

Intuitively, one can consider Rand index as a measure of the percentage of correct decisions made by the algorithm:

\[
RI = \frac{TP + TN}{TP + TN + FP + FN}
\]

where TP: number of true positives, TN: true negatives, FP: false positives, and FN: false negatives.

• Adjusted Rand Index (ARI): Measures the similarity between the true and predicted clusterings, adjusting for chance by normalizing the index to account for random partitions.

\[
ARI = \frac{RI – E[RI]}{\max(RI) – E[RI]}
\]
where RI: The Rand index value, E: The expected value of the Rand index for random clusters, and max(RI): The maximum achievable value of the Rand index (always 1).

• Normalized Mutual Information (NMI): Quantifies the amount of information obtained about one clustering from the other, normalized between 0 and 1.

2. Internal Evaluation Metrics

Internal metrics examine the clustering structure without needing ground truth. Common internal metrics include:

• Silhouette Score: Measures how similar an object is to its own cluster compared to other clusters. The silhouette score ranges from -1 to 1, with higher values indicating better-defined clusters.

\[
s(i) = \frac{b(i) – a(i)}{\max(a(i), b(i))}
\]

where \(a(i)\) is the average distance from point \(i\) to all other points in the same cluster, and \( b(i) \) is the minimum average distance from \( i \) to points in a different cluster.

• Dunn Index: Evaluates the ratio of the minimum inter-cluster distance to the maximum intra-cluster distance. Higher Dunn Index values indicate better clustering.

\[
Dunn = \frac{\min_{i \neq j} d(C_i, C_j)}{\max_k d(C_k)}
\]

where \(d(C_i, C_j)\) is the distance between cluster centroids.

• Calinski-Harabasz Index: Also known as the variance ratio criterion, it computes the ratio of the sum of between-cluster dispersion to within-cluster dispersion.

Applications of Clustering

• Market Segmentation: Businesses employ clustering to identify distinct consumer segments, enabling targeted marketing strategies and personalized services.
• Image Segmentation: In computer vision, clustering techniques segment images into different regions for analysis, allowing for object detection and recognition.
• Social Network Analysis: Clustering is utilized to recognize communities within social networks, enabling the identification of influencers and strong ties among users.
• Anomaly Detection: By identifying clusters of “normal” behavior, unusual observations can be flagged as potential anomalies.

Closing Remarks

While clustering remains an unsupervised technique, the importance of combining it with domain knowledge, constraints, and appropriate interpretations cannot be overstated. Ongoing research into robust clustering techniques, especially concerning scalability, interpretability, and high-dimensional data, will undoubtedly shape the future landscape of data analysis.

Resources

• Rand index wiki
• Silhouette score wiki