Byte Pair Encoding (BPE) Explained: How It Fuels Powerful LLMs

Traditional tokenization techniques face limitations with vocabularies, particularly with respect to unknown words, out-of-vocabulary (OOV) tokens, and the sparsity of tokens. Herein lies the significance of BPE: it offers a means of balancing vocabulary size and token representational accuracy, addressing many of the deficiencies presented by classical tokenization approaches.

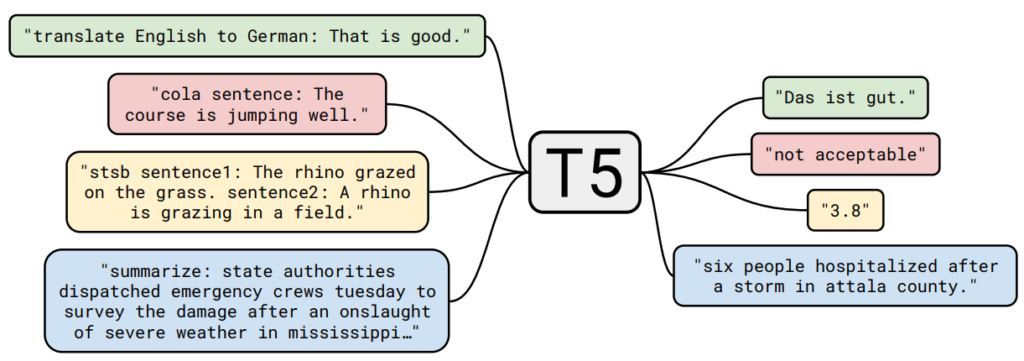
Originally conceived as a text compression method, Byte Pair Encoding (BPE) has been effectively adapted for tokenization and vocabulary management within NLP models. It is employed by different Transformer models such as GPT, RoBERTa, BART, and DeBERTa.

History and Development of BPE

Byte Pair Encoding was initially introduced by Philip Gage in 1994, primarily as a lossless data compression technique. The approach exploits the frequency of pairs of adjacent symbols (or bytes) in a dataset, repeatedly merging the most common pairs until a specified dictionary size is achieved or no more pairs are available.

Sennrich et al. (2015) popularized its usage in neural machine translation (NMT) to manage vocabulary size effectively while ensuring contextually relevant token representations. By creating subword units from the text corpus, BPE minimizes the risk of OOV issues that arise in conventional tokenization methods and improves model performance on various nuances within languages.

Mechanism of BPE

The implementation of BPE is rooted in a few core steps, encapsulated as follows:

1. Initial Tokenization: The input text is initially represented as a sequence of characters, where each character is treated as a unique token. Spaces between words are usually preserved.
2. Frequency Count: The next step is to count the frequencies of all adjacent symbol pairs in the text.
3. Merging Pairs: The most frequently occurring byte pair is identified. This byte pair is then merged into a single new token (or composite symbol), effectively replacing all instances of the pair in the text.
4. Iteration: Steps 2 and 3 are iteratively repeated until the stopping criteria is met. Each iteration reduces the character sequence size while forming new, more complex symbols/subwords.
5. Stopping Condition: The process continues until: (a) A predefined vocabulary size is reached, (b) A specified number of merges has been executed, or (c) The frequency of the next most common pair falls below a threshold.

BPE Algorithm: Pseudocode

function BPE(text, num_merges):
    # Step 1: Initialize tokens with characters and word boundaries (spaces)
    tokens = initialize_tokens(text)  # Splits text into words and then characters
    vocab = set(tokens) # Use a set for efficient membership checking
    
    for i from 1 to num_merges:
        # Step 2: Count pair frequencies within words
        pair_freq = {}
        for word in tokens: # Process each word separately
            for j from 0 to len(word) - 2:
                pair = (word[j], word[j+1])
                pair_freq[pair] = pair_freq.get(pair, 0) + 1

        # Step 3: Identify the most frequent pair
        if not pair_freq: # Handle edge case where no more pairs can be merged
            break
        most_frequent_pair = max(pair_freq, key=pair_freq.get)

        # Step 4: Merge the most frequent pair into a new symbol
        new_symbol = "".join(most_frequent_pair) # Concatenate for the new symbol
        vocab.add(new_symbol)

        # Step 5: Replace the most frequent pair with the new symbol in tokens
        new_tokens = []
        for word in tokens:
            new_word = word.replace("".join(most_frequent_pair), new_symbol) # Efficient string replacement
            new_tokens.append(new_word)
        tokens = new_tokens

    return tokens, vocab

Example Walkthrough

Let’s walk through the BPE algorithm with the text “hickory dickory dock“.

Step 1: Initial Tokenization

We start by splitting the text into words and then further into characters, including spaces as word boundaries.

Tokens: ['h', 'i', 'c', 'k', 'o', 'r', 'y', ' ', 'd', 'i', 'c', 'k', 'o', 'r', 'y', ' ', 'd', 'o', 'c', 'k']

Initial Vocabulary: {'h', 'i', 'c', 'k', 'o', 'r', 'y', ' ', 'd'}

Step 2: Counting Pair Frequencies (Iteration 1)

We count the occurrences of adjacent character pairs within each word:

• “hickory”: hi:1, ic:1, ck:1, ko:1, or:1, ry:1
• “dickory”: di:1, ic:1, ck:1, ko:1, or:1, ry:1
• “dock”: do:1, oc:1, ck:1

Pair Frequencies: {'hi': 1, 'ic': 2, 'ck': 3, 'ko': 2, 'or': 2, 'ry': 2, 'do': 1, 'oc': 1}

Step 3: Merging the Most Frequent Pair (Iteration 1)

The most frequent pair is “ck” (3 occurrences). We merge it into a new token.

New Token: “ck”

Updated Tokens: ['h', 'i', 'ck', 'o', 'r', 'y', ' ', 'd', 'i', 'ck', 'o', 'r', 'y', ' ', 'd', 'o', 'ck']

Updated Vocabulary: {'h', 'i', 'c', 'k', 'o', 'r', 'y', ' ', 'd', 'ck'}

Step 2: Counting Pair Frequencies (Iteration 2)

• “hickory”: hi:1, i ck:1, ck o:1, or:1, ry:1
• “dickory”: di:1, i ck:1, ck o:1, or:1, ry:1
• “dock”: do:1, o ck:1

Pair Frequencies: {'hi': 1, 'i ck': 2, 'ck o': 2, 'or': 2, 'ry': 2, 'do': 1}

Step 3: Merging the Most Frequent Pair (Iteration 2)

The most frequent pairs are “i ck”, “ck o”, “or”, and “ry” all with 2 occurrences. We can choose any of them. Let’s choose “i ck”.

New Token: “ick”

Updated Tokens: ['h', 'ick', 'o', 'r', 'y', ' ', 'd', 'ick', 'o', 'r', 'y', ' ', 'd', 'o', 'ck']

Updated Vocabulary: {'h', 'i', 'c', 'k', 'o', 'r', 'y', ' ', 'd', 'ck', 'ick'}

Step 2: Counting Pair Frequencies (Iteration 3)

• “hickory”: h ick:1, ick o:1, or:1, ry:1
• “dickory”: d ick:1, ick o:1, or:1, ry:1
• “dock”: do:1, o ck:1

Pair Frequencies: {'h ick': 1, 'ick o': 2, 'or': 2, 'ry': 2, 'd ick': 1, 'do': 1, 'o ck': 1}

Step 3: Merging the Most Frequent Pair (Iteration 3)

“ick o”, “or” and “ry” have the highest frequency. Let’s choose “or”.

New Token: “or”

Updated Tokens: ['h', 'ick', 'or', 'y', ' ', 'd', 'ick', 'or', 'y', ' ', 'd', 'o', 'ck']

Updated Vocabulary: {'h', 'i', 'c', 'k', 'o', 'r', 'y', ' ', 'd', 'ck', 'ick', 'or'}

And so on. You can continue this process for a set number of merges or until a certain frequency threshold is met.

Example after a few more merges (Illustrative):

Let’s imagine after a few more steps we have merged “h ick” to “hick” and “d ick” to “dick”.

Tokens: ['hick', 'ory', ' ', 'dick', 'ory', ' ', 'd', 'o', 'ck']

Vocabulary (Example): {'h', 'i', 'c', 'k', 'o', 'r', 'y', ' ', 'd', 'ck', 'ick', 'or', 'ory', 'hick', 'dick'}

This detailed walkthrough should give you a clear understanding of how BPE works. Remember that the exact final vocabulary will depend on how many merge operations you perform.

Advantages of Byte Pair Encoding

1. Reduced Vocabulary Size: BPE considerably shrinks the size of learned vocabularies compared to traditional word-level tokenization, which is particularly beneficial when dealing with extensive corpora.
2. Handling Morphological Variation: The algorithm’s capacity to represent morphological variations of words effectively reduces the risk of losing semantic information, leading to better performance in NLP tasks.
3. Scalability: Given its efficiency, BPE scales seamlessly across diverse applications, from simple text classification to complex sequence modeling tasks.
4. Custom Vocabulary Sizes: BPE allows practitioners to choose various vocabulary sizes based on application needs and the ratio of subword to word tokens.
5. Language Agnosticism: The BPE approach is language-agnostic, making it applicable across numerous linguistic contexts and effectively addressing the challenges presented by low-resource languages.
6. Reduction of OOV Issues: By utilizing subword units, BPE dramatically decreases the occurrences of OOV tokens. This is crucial for models that deal with rich morphologies, as it allows the model to form a valid representation of previously unseen words.
7. Applicability Across Languages: BPE’s effectiveness is demonstrated across a wide spectrum of languages, providing a tool for multilingual models. Its ability to handle various linguistic rules and variations makes it an ideal candidate for global applications.
8. Improved Generalization: By lessening the dependence on entire words, BPE promotes improved generalization, allowing models to extrapolate meanings even from unseen combinations of subwords.
9. Contextual Understanding: By implementing a subword-based vocabulary, models like BERT and GPT are capable of understanding and generating text with complex word forms and morphological variations.

Limitations of BPE

1. Algorithmic Complexity: While BPE is less complex than some other methods, the iterative procedure requires managing pair frequencies across potentially large datasets, introducing some degree of computational overhead.
2. Loss of Information: In defining subword units, BPE may also lead to a loss of semantic information. For instance, splitting common phrases or idiomatic expressions may result in the loss of contextual significance during the training of models that would otherwise benefit from understanding such expressions in their entirety.
3. Over-segmentation: Excessive segmentation may occur based on the dataset’s frequency distribution, where commonly used phrases may be split into less informative units, diluting their significance and complicating downstream tasks.
4. Non-Intuitive Splits: BPE may generate subword units that do not align with linguistic boundaries, potentially resulting in artifact tokens that obscure meaning during downstream processing.
5. Dependency on Frequency: BPE’s effectiveness is highly dependent on the frequency of word pairs. Rare words or pairs may not be captured efficiently, leading to potential biases in representation.

Reference:
1. huggingface-nlp-course
2. keras