How To Compute The Token Consumption Of Vision Transformers?

To compute the number of tokens in a Vision Transformer (ViT), it’s essential to understand how images are processed and transformed into tokens within the architecture.

Here’s a step-by-step explanation using an example based on the provided context.

Understanding Vision Transformers

Vision Transformers (ViTs) leverage the Transformer architecture, originally designed for natural language processing, to perform image recognition tasks. The process involves several key steps (best explained here):

1. Patch Extraction: The input image is divided into smaller, non-overlapping patches.
2. Linear Projection: Each patch is flattened and projected into a fixed-dimensional embedding space using a linear layer.
3. Positional Embedding: Since Transformers lack inherent positional awareness, positional embeddings are added to the patch embeddings to retain spatial information.
4. Transformer Encoding: The sequence of embedded patches is processed through multiple Transformer blocks, which include mechanisms like self-attention and feed-forward networks.
5. Classification Head: The final representation from the Transformer is fed into a classification layer to predict the image label.

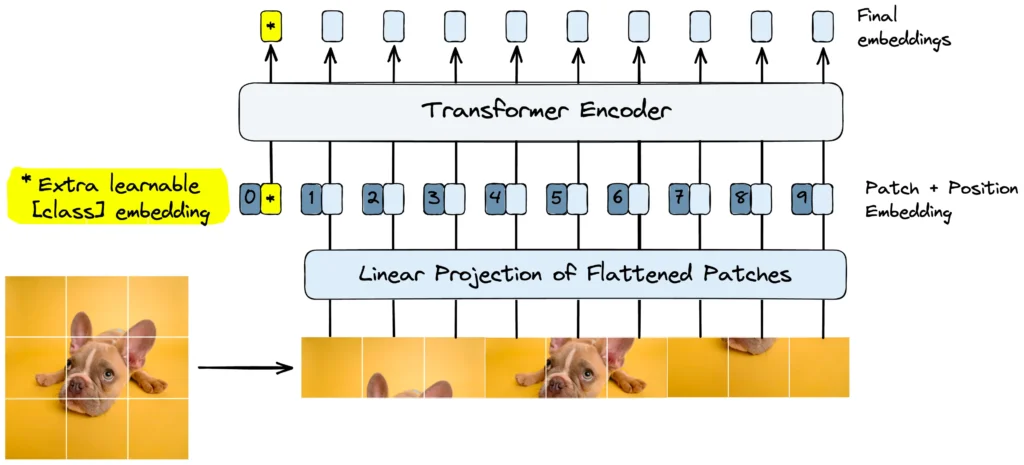
Computing the Number of Tokens

Tokens in the context of Vision Transformers refer to the embedded representations of image patches. The number of tokens is directly determined by how the image is partitioned into patches.

Step-by-Step Example

Let’s compute the number of tokens using the following parameters:

• Image Size: 224×224 pixels
• Patch Size: 16×16 pixels

1. Determine the Number of Patches per Dimension
   • Width: The image width is divided by the patch width.
     \[
     \text{Number of patches along width} = \frac{224}{16} = 14
     \]
   • Height: Similarly, the image height is divided by the patch height.
     \[
     \text{Number of patches along height} = \frac{224}{16} = 14
     \]
2. Calculate the Total Number of Patches (Tokens)
   • Multiply the number of patches along the width by the number of patches along the height.
     \[
     \text{Total number of patches} = 14 \times 14 = 196
     \]
   • Result: For a 224×224 image with 16×16 patches, there are 196 tokens.

Visualization

Imagine dividing a 224×224 image into a grid of 16×16 patches:

+--------+--------+--------+ ...    +---------+  
| Patch1 | Patch2 | Patch3 | ...    | Patch14 |  
+--------+--------+--------+ ...    +---------+  
| Patch15| Patch16| Patch17| ...    | Patch28 |  
+--------+--------+--------+ ...    +---------+  
|  ...   |  ...   |  ...   | ...    |  ...    |  
+--------+--------+--------+ ...    +---------+  
| Patch183| Patch184| Patch185| ... | Patch196|  
+--------+--------+--------+ ...    +---------+  

Each Patch represents a 16×16 segment of the original image, and each patch becomes a token after linear projection.

Impact of Patch and Image Sizes on Token Count

The number of tokens increases with higher image resolutions or smaller patch sizes. Here’s how different configurations affect the token count:

1. Higher Image Resolution
   • Example: 448×448 image with 16×16 patches will result in \( 28 \times 28 = 784 \) tokens.
   • Result: Doubling the image resolution quadruples the number of tokens.
2. Smaller Patch Size
   • Example: 224×224 image with 8×8 patches will also result in \(28 \times 28 = 784\) tokens.
   • Result: Halving the patch size increases the number of tokens by four times.

Memory Footprint Considerations

Each additional token increases the memory required for processing, especially during the self-attention computation in Transformer blocks, which scales quadratically with the number of tokens. Therefore, there’s a trade-off between the granularity of image representation (smaller patches lead to more tokens and finer detail) and computational efficiency (fewer tokens are faster and require less memory).

Summary

• Formula to Compute Tokens:
  \[
  \text{Number of Tokens} = \left( \frac{\text{Image Width}}{\text{Patch Width}} \right) \times \left( \frac{\text{Image Height}}{\text{Patch Height}} \right)
  \]
• Example Computation:For a 224×224 image with 16×16 patches:
  \[
  \frac{224}{16} = 14 \text{ patches per dimension} \
  14 \times 14 = 196 \text{ tokens}
  \]