Imagine you are a master artist, renowned for creating breathtaking paintings with an infinite palette of colors. Your paintings are rich, detailed, and full of subtle nuances. Now, you are asked to reproduce your masterpiece, but with a limited set of just 256 crayons. If you simply try to map each of your infinite colors to the closest crayon color after the painting is finished, the result might be disappointing. Colors will clash, and the subtle gradients that made your work special will be lost, turning into harsh, distinct bands. This is what happens in Post-Training Quantization (PTQ).
But what if you knew about the 256-crayon limitation from the start? You could adapt your artistic process. You would intentionally choose colors and techniques that work well with the limited palette, perhaps using dithering to create the illusion of more colors. Your final crayon-based artwork would look far superior to the first attempt. This is the core idea behind Quantization-Aware Training (QAT).
Quantization, in the context of deep learning, is the process of reducing the precision of a model’s numbers (weights and activations) from high-precision floating-point numbers (like 32-bit floats) to low-precision integers (like 8-bit integers). This makes models smaller, faster, and more energy-efficient—critical for deployment on devices like smartphones or embedded systems. QAT is a technique that simulates this low-precision environment during the training or fine-tuning process, allowing the model to adapt and mitigate the accuracy loss that simple quantization can cause.
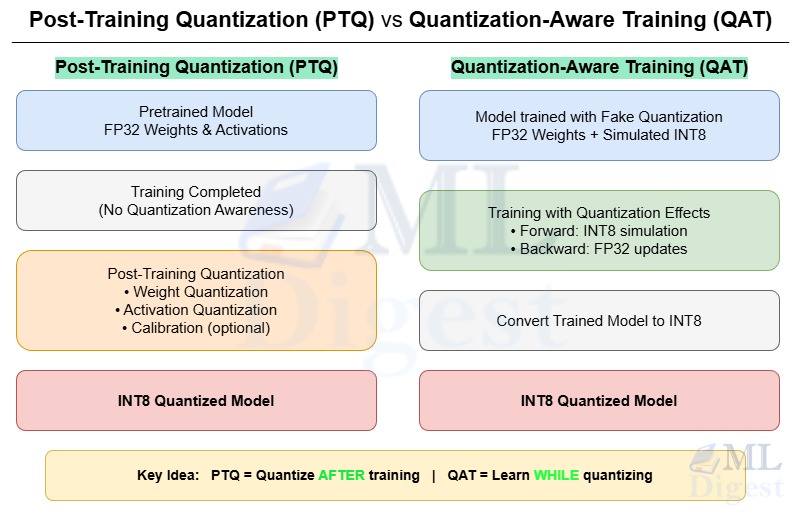
The Limits of Post-Training Quantization (PTQ)
The simplest way to quantize a model is Post-Training Quantization (PTQ). You take a fully trained, high-precision model and then convert its weights to a lower precision. It is fast and easy, but it can sometimes lead to a significant drop in accuracy.
Think of it like rounding numbers. If a model relies on very specific, high-precision weight values to make a decision, rounding those weights after the fact can drastically change its output. For many models, especially smaller or more sensitive ones, this accuracy drop is unacceptable.
Enter Quantization-Aware Training (QAT): Training for the Real World
QAT bridges the gap between high-performance, floating-point models and efficient, integer-based models. Instead of training in an ideal world of infinite precision and then suddenly forcing the model into a constrained one, QAT simulates the effect of quantization during the training process.
The model learns, from the very beginning, how to perform its task under the constraints of low-precision arithmetic. It is like a student who knows the final exam will be closed-book; they study by memorizing key facts, not by learning how to look things up efficiently. By fine-tuning the model with quantization in the loop, we teach it to be robust to the “noise” of quantization, resulting in a model that maintains high accuracy even after conversion to integers.
A Deeper Dive: The Mechanics of QAT
To understand how QAT works, we need to introduce a clever trick: “fake” quantization. During training, we cannot use real integer arithmetic because the rounding operation is non-differentiable, which means we cannot compute gradients and use backpropagation to update the model’s weights.
To solve this, QAT inserts special nodes or layers, often called Quantize-Dequantize (QDQ) or “fake quant” nodes, into the model graph. Here is how they work:
- Quantize: The floating-point weights and activations are scaled and rounded to simulate the effect of 8-bit integer representation.
- Dequantize: The “quantized” integer values are immediately scaled back to floating-point numbers.
This process, float -> int -> float, introduces the same quantization error that the model will experience during integer-only inference, but it keeps the data in a floating-point format so that the network can be trained with standard backpropagation.
The Straight-Through Estimator (STE)
But what about the gradient of the rounding function? It is zero almost everywhere, which would stop our model from learning. To overcome this, QAT uses a technique called the Straight-Through Estimator (STE).
The STE is a simple but powerful idea: during the forward pass, we use the quantized values, but during the backward pass, we pretend the rounding function was just an identity function. We pass the gradient straight through the rounding operation as if it never happened.
Mathematically, if q = round(x) is our quantization function, the forward pass uses q, but the backward pass uses a “fake” gradient:
$$
\frac{\partial C}{\partial x} \approx \frac{\partial C}{\partial q}
$$
This allows the gradients to flow back to the original floating-point weights, enabling the model to learn and adjust its weights to minimize the error caused by the quantization simulation. Optionally gradients can be clipped outside dynamic range to prevent extreme updates.
Implementing QAT: A Step-by-Step Guide
Implementing QAT typically follows these steps, supported by frameworks like PyTorch and TensorFlow.
- Start with a Pre-trained Model: You do not need to train from scratch. The best practice is to start with a well-performing, pre-trained floating-point model.
- Insert Fake Quantization Nodes: Modify the model architecture by inserting QDQ nodes at the boundaries of where you want to perform quantized operations. This is usually done for the inputs and outputs of convolutional and fully-connected layers.
- Fine-Tune the Model: With the QDQ nodes in place, you fine-tune the model for a few epochs. This is not full-scale training. You use a very low learning rate, as the goal is to adjust the already-trained weights to the new quantization constraint, not to re-learn the entire task.
- Convert to a True Quantized Model: After fine-tuning, the model is ready for conversion. The fake quantization nodes are removed, and the floating-point weights are converted to their final integer form, along with the learned scaling factors. The resulting model is now a truly quantized, efficient model ready for deployment.
Practical Tips and Best Practices
- QAT vs. PTQ: Always try PTQ first. If the accuracy drop is acceptable (e.g., <1%), you have saved yourself time. If not, QAT is the answer.
- Start with a Good Model: QAT cannot fix a poorly trained model. Your starting floating-point model should be as accurate as possible.
- Short Fine-Tuning: You only need to fine-tune for a small number of epochs (1-10 is common). The goal is to adapt, not to train from scratch.
- Low Learning Rate: Use a learning rate that is 10x to 100x smaller than what you used for the original training.
- Selective Quantization: Not all layers need to be quantized. Some models benefit from leaving the very first and very last layers in floating-point precision, as they are often the most sensitive. This is known as partial quantization.
LLM Quantization
Transformer-based models introduce activation outliers (e.g., attention score distributions) and precision sensitivity in LayerNorm and embedding layers. Strategies:
- Weight-only quantization (e.g., GPTQ, AWQ) focuses on compressing weights while retaining activations in higher precision to minimize accumulated rounding error.
- SmoothQuant redistributes activation scaling into weights to shrink activation magnitude variance, improving INT8 applicability without full QAT.
- QLoRA combines low-rank adapters with 4-bit quantization of base weights; adaptation occurs in a small parameter space while preserving core model performance.
- Partial quantization: keep first embedding layer and final projection in FP16/FP32; quantize intermediate linear and attention projections.
When full QAT is applied to transformers: carefully schedule observer freezing and consider per-channel quantization for linear layers. Monitor perplexity or task-specific metrics after each phase.
Conclusion
Quantization-Aware Training offers the best of both worlds: the high accuracy of floating-point models and the high performance of integer models. By simulating the effects of quantization during training, it allows the model to learn to be robust to precision loss, making it an indispensable tool for deploying state-of-the-art deep learning models on resource-constrained hardware. It turns the challenge of a limited crayon box into an opportunity for creating a different, yet equally beautiful, kind of masterpiece.
