Gradient Scaling: Improve Neural Network Training Stability

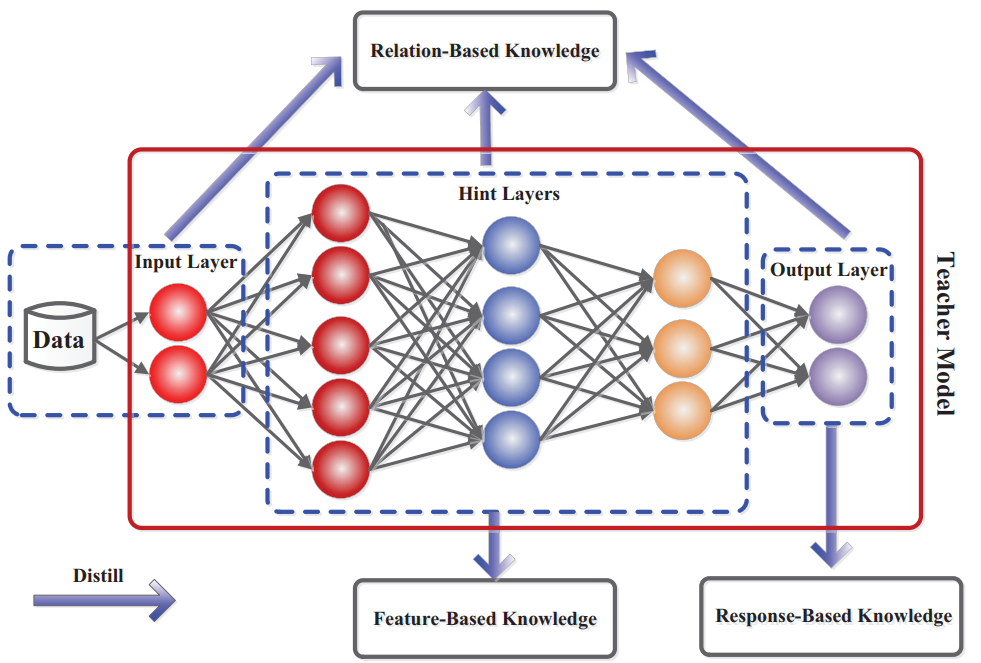
What is Gradient Scaling?

Gradient scaling is a technique primarily used to address numerical stability issues that arise during the training of neural networks, especially in mixed-precision training. It involves adjusting the scale of gradients to prevent them from underflowing (becoming too small) or overflowing (becoming too large) when represented in lower-precision formats like 16-bit floating-point (FP16).

The Need for Gradient Scaling

Traditional training of neural networks employs 32-bit floating-point (FP32) representations for computations and gradient storage. However, as models grow in size and complexity, mixed-precision training—where computations are performed in lower precision (e.g., FP16) while maintaining certain critical values in higher precision—has gained popularity.

In mixed-precision training, gradients computed in lower-precision formats are susceptible to:

• Underflow: Extremely small gradient values may become zero in FP16, leading to loss of crucial information and hindering learning.
• Overflow: Extremely large gradient values may exceed the representable range, resulting in infinite or undefined values.

Gradient scaling mitigates these issues by dynamically adjusting the magnitude of gradients during training, ensuring they remain within a representable and stable range.

How Gradient Scaling Works

Gradient scaling typically involves two primary steps:

1. Scaling the Loss: Before backpropagation, the loss is multiplied by a scaling factor.
2. Unscaling the Gradients: After backpropagation, the gradients are divided by the same scaling factor before being used by the optimizer.

This process ensures that gradients remain within a numerically stable range, preventing underflow and overflow during mixed-precision computations.

Step-by-Step Mechanism

1. Scale the Loss
   • Multiply the loss \( L \) by a scaling factor \( s \) (a large positive number, e.g.,\( 2^{16} \)).
   • Compute the scaled loss \( L’ = s \times L \).
2. Backward Pass with Scaled Loss
   • Perform backpropagation on \( L’ \) to compute the scaled gradients \( g’ = \frac{\partial L’}{\partial \theta} = s \times \frac{\partial L}{\partial \theta} = s \times g \), where \( g \) is the original gradient.
3. Unscale the Gradients
   • Divide the scaled gradients \( g’ \) by the scaling factor \( s \) to obtain the original gradients \( g \).
   • \( g = \frac{g’}{s} \).
4. Optimizer Step
   • Use the unscaled gradients \( g \) to update the model parameters via the optimizer.
5. Dynamic Scaling and Overflow Handling
   • Monitor gradients for overflow (e.g., gradients containing NaNs or infinities).
   • If an overflow is detected, reduce the scaling factor \( s \) to prevent future overflows.
   • If no overflow is detected for a certain number of steps, consider increasing \( s \) to maximize the benefits of gradient scaling.

This dynamic adjustment ensures that gradients are optimally scaled throughout training, balancing the benefits of mixed-precision computation with numerical stability.

Benefits of Gradient Scaling

1. Prevents Gradient Underflow: Ensures that small gradient values don’t underflow to zero in lower-precision representations, preserving essential learning signals.
2. Mitigates Gradient Overflow: Prevents excessively large gradients from resulting in infinities or NaNs, maintaining training stability.
3. Enables Efficient Mixed-Precision Training: Facilitates the use of lower-precision formats (e.g., FP16) without sacrificing numerical integrity, leading to faster computations and reduced memory usage.
4. Improves Training Stability: By maintaining gradients within a stable range, gradient scaling contributes to smoother convergence and robust learning across diverse models and datasets.

Advanced Gradient Scaling Techniques

Beyond basic gradient scaling, several advanced methodologies have been developed to enhance gradient management further, especially in complex training environments.

1. Static vs. Dynamic Loss Scaling

• Static Loss Scaling: Uses a fixed scaling factor throughout training. While simpler, it may require careful tuning and might not adapt well to varying gradient magnitudes across training steps.
  • Simpler to implement. Predictable behavior.
  • May require manual tuning of the scaling factor.
• Dynamic Loss Scaling: Adjusts the scaling factor based on the presence of gradient overflows or underflows, typically increasing it when training is stable and decreasing it upon detecting overflows.
  • Adaptive to training dynamics.
  • Reduces the need for manual tuning.
  • Slightly more complex to implement.

2. Layer-Wise Gradient Scaling

In complex architectures with layers exhibiting varying gradient behaviors, layer-wise gradient scaling can be employed to adjust scaling factors independently for different layers.

• Analyze gradient statistics for individual layers.
• Assign distinct scaling factors tailored to each layer’s gradient characteristics.
• Apply scaling and unscaling operations on a per-layer basis.

3. Combined Gradient Scaling and Clipping

Combining gradient scaling with gradient clipping can offer enhanced stability by both preventing underflow/overflow and limiting gradient magnitudes proactively.

• Apply gradient scaling followed by gradient clipping (e.g., norm-based clipping) to cap gradient magnitudes, preventing excessively large updates.
• Facilitates more controlled and stable training dynamics.

Empirical Evidence Supporting Gradient Scaling

• ResNet-50 Training: Utilizing Tensor Cores with mixed-precision training and dynamic loss scaling resulted in significant speedups (~3x) compared to pure FP32 training, maintaining model accuracy and stability.
• GPT-3: Implemented mixed-precision training with dynamic gradient scaling to manage the extensive gradient computations, enabling feasible training durations and resource usage.
• BERT Training: Employed mixed-precision training with gradient scaling to accelerate training times while maintaining robust performance, demonstrating the technique’s practical benefits.
• StyleGAN: Integrated gradient scaling within the training pipeline to stabilize GAN training, leading to higher-quality generated images and more consistent convergence.

Implementing Gradient Scaling in Practice

Gradient Scaling in PyTorch

PyTorch offers the torch.cuda.amp module, which includes GradScaler and autocast to simplify mixed-precision training with gradient scaling.

from torch.cuda.amp import GradScaler, autocast 

scaler = GradScaler()  
   
# Training loop with mixed precision and gradient scaling  
for epoch in range(num_epochs):  
    for inputs, targets in dataloader:  
        inputs, targets = inputs.cuda(), targets.cuda()  
          
        optimizer.zero_grad()  
          
        with autocast():  
            outputs = model(inputs)  
            loss = criterion(outputs, targets)  
          
        # Scale the loss and perform backpropagation  
        scaler.scale(loss).backward()  
          
        # Optionally, unscale the gradients and perform gradient clipping  
        scaler.unscale_(optimizer)  
        torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)  
          
        # Update the optimizer and scaler  
        scaler.step(optimizer)  
        scaler.update()  

Gradient Scaling in TensorFlow

TensorFlow 2.x incorporates mixed-precision training capabilities via the tf.keras.mixed_precision API, which includes dynamic loss scaling for gradient scaling.

# Enable mixed precision  
policy = mixed_precision.Policy('mixed_float16')  
mixed_precision.set_policy(policy)  
   
# Wrap the optimizer with a loss scale optimizer  
optimizer = mixed_precision.LossScaleOptimizer(optimizer, loss_scale='dynamic')  
   
# Training loop with mixed precision and gradient scaling  
for epoch in range(num_epochs):  
    for inputs, targets in dataset:  
        with tf.GradientTape() as tape:  
            logits = model(inputs, training=True)  
            loss = loss_fn(targets, logits)  
          
        # Compute scaled gradients  
        scaled_loss = optimizer.get_scaled_loss(loss)  
        scaled_gradients = tape.gradient(scaled_loss, model.trainable_variables)  
          
        # Unscale gradients  
        gradients = optimizer.get_unscaled_gradients(scaled_gradients)  
          
        # Optionally, apply gradient clipping  
        gradients, _ = tf.clip_by_global_norm(gradients, 1.0)  
          
        # Apply gradients to optimizer  
        optimizer.apply_gradients(zip(gradients, model.trainable_variables)) 

Closing Remarks

Gradient scaling is an imporatant innovation for managing gradient magnitudes, primarily in the context of mixed-precision training. Integrating gradient scaling with other gradient management strategies, such as gradient clipping and adaptive optimizers, can further enhance training robustness and efficiency.

References

• Mixed Precision Training paper
• NVIDIA Documentation