Gradient Clipping: A Key To Stable Neural Networks

Training deep neural networks is a complex optimization process that relies on the effective management of gradients. Gradients guide the adjustment of model parameters to minimize loss functions. However, the intricate architecture of deep networks can lead to challenges such as gradient explosion and gradient vanishing, which significantly hamper the training process. Gradient clipping emerges as a pivotal technique to mitigate these issues, ensuring that gradients remain within a manageable range and thereby fostering stable and efficient learning.

What is Gradient Clipping?

Gradient clipping is a technique designed to prevent the gradients from becoming too large during training. By imposing a threshold on the gradients, this method ensures that their magnitudes remain within a predefined range, thereby stabilizing the training process and promoting efficient convergence.

Gradient clipping does not alter the underlying architecture or the optimization algorithm but acts as a safeguard to maintain gradient values within manageable limits.

Why is Gradient Clipping Important?

1. Prevents Numerical Instability: Excessively large gradients can lead to numerical issues, such as overflow errors, especially when combined with high learning rates.
2. Ensures Controlled Parameter Updates: By limiting gradient magnitudes, gradient clipping ensures that updates to model parameters are neither too drastic nor erratic, promoting smoother and more predictable learning trajectories.
3. Facilitates Training of Deep Networks: In architectures with many layers or recurrent connections, gradient clipping is essential to maintain stability and prevent divergence during backpropagation.
4. Improves Generalization: Controlled gradient updates can lead to better generalization by avoiding overshooting minima in the loss landscape.

Types of Gradient Clipping

There are primarily two methods for implementing gradient clipping: Value-Based Clipping and Norm-Based Clipping.

1. Value-Based Clipping

Value-based clipping involves restricting each individual component of the gradient vector to lie within a specified range. For example, if a gradient component exceeds a defined maximum value or falls below a minimum value, it is clipped to those thresholds.

Algorithm:

Given a gradient vector \( g \) and a clipping value \( c \), each component \( g_i \) is adjusted as follows:

\[
g_i = \begin{cases}
c & \text{if } g_i > c \\
g_i & \text{if } -c \leq g_i \leq c \\
-c & \text{if } g_i < -c
\end{cases}
\]

Pros:

• Simple to implement.
• Provides direct control over the range of gradient values.

Cons:

• Can distort the gradient direction, as different components may be clipped differently.
• Less effective in scenarios where the overall gradient norm needs control rather than individual components.

2. Norm-Based Clipping

Norm-based clipping scales the entire gradient vector if its norm exceeds a predefined threshold. This method preserves the direction of the gradient while controlling its magnitude.

Algorithm:

Given a gradient vector \( g \), compute its norm \( |g| \). If \( |g| > c \), scale the gradient as follows:

\[
g_{\text{clipped}} = g \times \frac{c}{|g|}
\]

Otherwise, leave the gradient unchanged.

Pros:

• Maintains the direction of the gradient, which is crucial for effective optimization.
• More widely used in practice, especially for training deep and complex networks.

Cons:

• Requires computation of the gradient norm, which can add computational overhead, albeit minimal.

Choosing Between Value-Based and Norm-Based Clipping

While both methods aim to control gradient magnitudes, norm-based clipping is generally preferred, especially in deep learning contexts, due to its ability to maintain the gradient’s directional integrity. This preservation is vital for the optimizer to make meaningful and directionally consistent updates to the model parameters.

When to Use Gradient Clipping

Gradient clipping is particularly beneficial in scenarios where the training process is prone to instability due to large gradients. Common use cases include:

1. Training Recurrent Neural Networks (RNNs): RNNs are especially susceptible to gradient explosion and vanishing, making gradient clipping essential.
2. Deep Networks with Many Layers: As the depth of the network increases, the risk of gradient-related issues escalates.
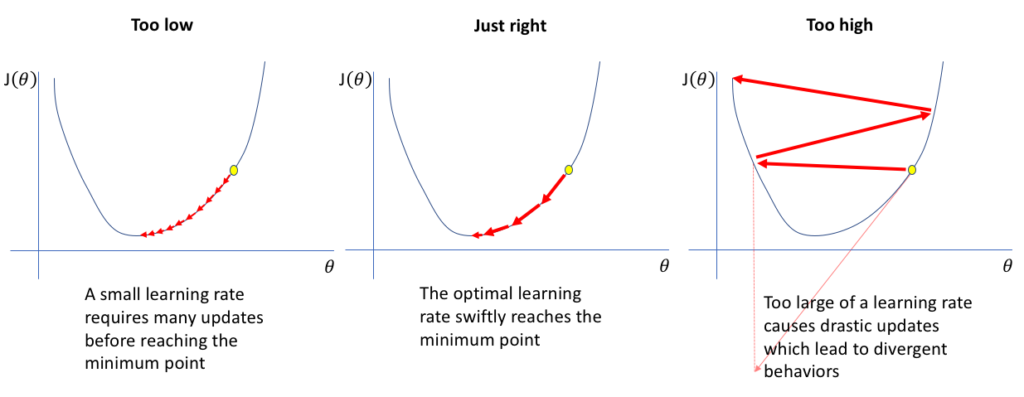
3. High Learning Rates: Large learning rates can cause rapid gradient updates, leading to instability. Gradient clipping can counteract this effect.
4. Complex Architectures: Models with intricate connectivity patterns or architectural nuances may benefit from controlled gradient magnitudes.
5. Training with Noisy Data: Noisy or unbalanced datasets can produce erratic gradients that destabilize training, where clipping can provide a stabilizing effect.

Benefits of Gradient Clipping

1. Enhanced Stability: By preventing excessively large gradients, gradient clipping ensures that the training process remains stable and does not diverge.
2. Improved Convergence: Controlled gradients facilitate smoother and more consistent convergence toward minima in the loss landscape.
3. Preventing Parameter Explosions: Large gradients can lead to exceedingly large parameter updates, causing parameters to take on infinite or undefined values. Clipping mitigates this risk.
4. Facilitating Higher Learning Rates: With gradient clipping in place, higher learning rates can be employed without the associated risk of instability, potentially accelerating training.

Limitations and Considerations

While gradient clipping is a powerful tool, it is not without limitations:

1. Potential Distortion of Gradient Information: Excessive clipping can distort the true gradient direction, potentially hindering the learning process.
2. Hyperparameter Tuning: Determining the optimal clipping threshold requires experimentation and can be dataset and model-dependent.
3. Performance Overhead: While minimal, gradient clipping introduces additional computational steps.

Advanced Gradient Clipping Techniques

Beyond the basic gradient clipping methods, several advanced strategies have been developed to enhance gradient management:

1. Adaptive Gradient Clipping

Adaptive gradient clipping dynamically adjusts the clipping threshold based on properties of the gradients or the training dynamics. This adaptability can lead to more nuanced control over gradient magnitudes, optimizing the balance between stability and learning efficacy.

• Monitor gradient statistics, such as mean and standard deviation.
• Adjust the clipping threshold in response to changes in these statistics.
• Employ algorithms that adaptively tweak the threshold to maintain optimal gradient scales.

2. Layer-Wise Gradient Clipping

In complex networks, different layers may exhibit varying gradient behaviors. Layer-wise gradient clipping assigns distinct clipping thresholds to different layers, accommodating their unique gradient distributions.

• Analyze gradient norms for individual layers.
• Set specific clipping thresholds tailored to each layer’s gradient characteristics.
• Apply clipping independently for each layer based on its designated threshold.

3. Gradient Centralization

Gradient centralization involves shifting gradients to have zero mean along certain dimensions. This technique can improve the optimization landscape, potentially leading to better convergence properties.

• Compute the mean of gradients along specified dimensions.
• Subtract this mean from the gradients to center them around zero.
• Optionally, combine with gradient clipping for enhanced stability.

4. Utilizing Optimizer-Specific Clipping Mechanisms

Some optimizers incorporate their own gradient clipping mechanisms or can be extended to support advanced clipping strategies. Exploring optimizer-specific features can provide more seamless and efficient integration of gradient clipping.

• AdamW: An optimizer that decouples weight decay from the gradient update, which can be combined with gradient clipping for improved regularization and stability.

Empirical Evidence Supporting Gradient Clipping

• Long Short-Term Memory (LSTM) Networks: Incorporating gradient clipping in LSTM training has been essential for tasks like language modeling and sequence prediction, enabling the networks to learn long-term dependencies without diverging.
• Residual Networks (ResNets): ResNets, with their skip connections and deep architectures, benefit from gradient clipping to prevent vanishing or exploding gradients, facilitating the training of extremely deep models (e.g., ResNet-152).
• Original Transformer Model: In the seminal “Attention is All You Need” paper, gradient clipping was employed with a norm threshold of 1.0 to stabilize training, highlighting its integral role even in cutting-edge architectures.
• Wasserstein GANs (WGANs): Gradient clipping was originally introduced in WGANs to enforce the Lipschitz constraint, ensuring stable training dynamics.

Practical Tips for Effective Gradient Clipping

To maximize the benefits of gradient clipping while minimizing potential drawbacks, consider the following best practices:

• Start with Common Defaults: Begin with widely used thresholds (e.g., 1.0 or 5.0) and adjust based on model performance and training behavior.
• Monitor Training Metrics: Observe loss trajectories and gradient norms to inform adjustments to the clipping threshold.
• Avoid Excessive Clipping: Setting the threshold too low can impede learning by overly restricting gradient magnitudes.
• Learning Rate Schedules: Integrate gradient clipping with adaptive learning rate schedules (e.g., learning rate warm-up) for synergistic stabilization.
• Regularization Methods: Use alongside regularization techniques like dropout or weight decay to enhance generalization and prevent overfitting.
• Track Gradient Norms: Keep a record of gradient norms during training to assess the effectiveness of clipping and identify emerging issues.
• Visualize Gradient Distributions: Utilize tools like TensorBoard to visualize gradients, ensuring they remain within expected ranges.

Implementing Gradient Clipping

Example: Norm-Based Gradient Clipping in PyTorch

 # Training loop with gradient clipping  
for epoch in range(num_epochs):  
    for inputs, targets in dataloader:  
        optimizer.zero_grad()  
        outputs = model(inputs)  
        loss = criterion(outputs, targets)  
        loss.backward()  
          
        # Apply norm-based gradient clipping with a max norm of 2.0  
        torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=2.0)  
          
        optimizer.step()  

Example: Norm-Based Gradient Clipping in TensorFlow 2.x

# Training loop with gradient clipping  
for epoch in range(num_epochs):  
    for inputs, targets in dataset:  
        with tf.GradientTape() as tape:  
            logits = model(inputs, training=True)  
            loss = loss_fn(targets, logits)  
          
        gradients = tape.gradient(loss, model.trainable_variables)  
          
        # Apply norm-based gradient clipping with a max norm of 2.0  
        clipped_gradients, _ = tf.clip_by_global_norm(gradients, 2.0)  
          
        optimizer.apply_gradients(zip(clipped_gradients, model.trainable_variables))  

Gradient Clipping vs. Other Gradient Management Techniques

While gradient clipping is a robust technique for managing gradient magnitudes, it is one of several tools available for ensuring training stability. Understanding how it compares and complements other methods is crucial for effective training.

1. Gradient Clipping vs. Gradient Normalization

• Gradient Clipping: Directly modifies gradients that exceed a certain threshold to prevent explosion.
• Gradient Normalization: Adjusts gradients to have a specific norm, ensuring consistency in their scale without introducing hard thresholds.
• Gradient normalization maintains gradient scales more uniformly, whereas clipping imposes strict limits that can be more disruptive if not carefully tuned.

2. Gradient Clipping vs. Adaptive Optimization Algorithms

• Adaptive Optimizers: Algorithms like Adam, RMSProp, and Adagrad adaptively adjust learning rates based on gradient statistics, inherently helping to manage gradient magnitudes.
• Gradient Clipping: Acts as an additional safeguard on top of these optimizers, providing explicit control over gradient scales.
• While adaptive optimizers mitigate some gradient issues, gradient clipping provides an extra layer of protection, particularly in scenarios where optimizer adaptations are insufficient.

3. Gradient Clipping vs. Regularization Techniques

• Regularization: Methods like L1/L2 regularization, dropout, and batch normalization aim to prevent overfitting and improve generalization.
• Gradient Clipping: Specifically targets gradient explosion and vanishing, focusing on maintaining optimization stability.
• These techniques address different aspects of model training; however, they can be complementary. For instance, regularization methods can be used alongside gradient clipping to ensure both stable optimization and robust generalization.

4. Gradient Clipping vs. Weight Initialization

• Weight Initialization: Proper initialization schemes (e.g., Xavier, He) can help in preventing gradient vanishing or explosion at the outset.
• Gradient Clipping: Provides ongoing management of gradients during training, beyond the initial phases.
• Good weight initialization reduces the risk of early gradient issues, while gradient clipping ensures continued stability as training progresses, especially as the model encounters more complex data patterns.

Closing Remarks

It is crucial to implement gradient clipping judiciously, balancing its benefits against potential drawbacks such as the distortion of gradient information. By integrating gradient clipping with other optimization strategies, monitoring training metrics, and adapting clipping thresholds as needed, practitioners can harness its full potential to develop high-performing and reliable neural networks.

References

• Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press. Link
• neptune.ai post