Two critical issues that often arise in training deep neural networks are vanishing gradients and exploding gradients. These issues can drastically affect the performance and stability of the model.
Understanding Backpropagation and Gradients
Before discussing vanishing and exploding gradients, it’s crucial to understand backpropagation, the core algorithm used to train neural networks. Backpropagation calculates the gradient of the loss function with respect to each weight in the network. This gradient indicates the direction and magnitude of the steepest ascent of the loss function. During training, we adjust the weights in the opposite direction of the gradient to minimize the loss, effectively finding the optimal parameters for our model.
These gradients indicate how much change in each parameter is required to reduce the loss. If the gradient is too small or too large, it can prevent the model from effectively learning or cause the learning process to become unstable. This is where vanishing and exploding gradients come into play.
Vanishing Gradients: When Learning Slows to a Crawl
The vanishing gradient problem arises when the gradient becomes extremely small during backpropagation, especially in deep networks with many layers. As we propagate the gradient backward from the output layer to the earlier layers, it gets multiplied by the weights and the derivatives of the activation functions at each layer.
For any activation function, the absolute value of the weight updates (dW) tends to decrease as we move backward through the layers. This is particularly pronounced in deep networks. Consequently, the weights of the earlier layers are updated very slowly, leading to slow convergence. In severe cases, the earlier layers may barely learn at all, effectively halting the training process.
Causes of Vanishing Gradients
- Saturated Activation Functions: Functions like the sigmoid and tanh are prone to vanishing gradients because their derivatives are small in certain regions. For instance, the sigmoid function has a range between 0 and 1, and its derivative approaches zero as the function value approaches these extremes. As the gradient is propagated through many layers, the small values can diminish exponentially.
- Deep Networks: In very deep networks, the repeated multiplication of small gradients (especially when using saturated activation functions) causes the overall gradient to shrink, resulting in vanishing gradients.
- Initialization Issues: Poor initialization of weights can exacerbate the vanishing gradient problem. If the weights are initialized to small values, the gradients can shrink even further during backpropagation.
Solutions to Vanishing Gradients
- ReLU Activation Function: The Rectified Linear Unit (ReLU) and its variants (e.g., Leaky ReLU, Parametric ReLU) are popular alternatives to sigmoid and tanh because they do not saturate in the positive domain. ReLU outputs the input directly if it’s positive and zero otherwise. Its derivative is 1 for positive inputs and 0 for negative inputs. This simple property helps maintain a stronger gradient during backpropagation, mitigating the vanishing gradient issue. While ReLU can still suffer from “dying ReLU” (neurons getting stuck with zero output), variations like Leaky ReLU and Parametric ReLU address this issue.
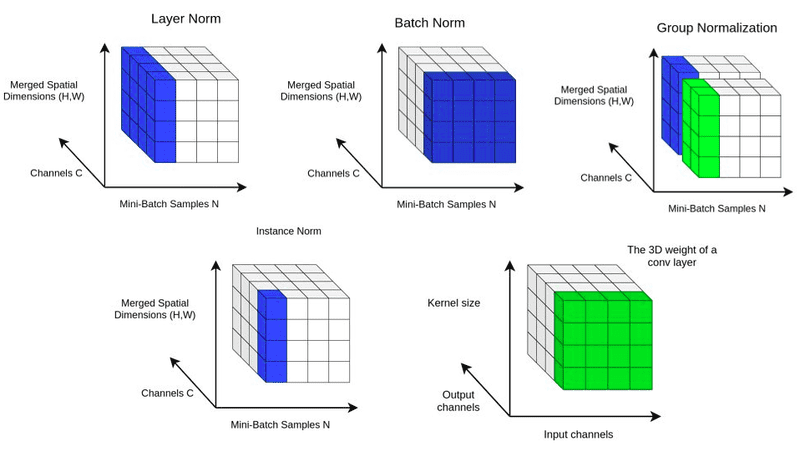
- Batch Normalization: This technique normalizes the inputs to each layer, helping gradients to remain at a reasonable scale throughout the network.
- Weight Initialization: Proper weight initialization schemes, like Xavier/Glorot initialization and He initialization, are designed to prevent gradients from becoming too small by considering the network’s architecture and the activation function’s properties.
Exploding Gradients: When Learning Becomes Unstable
Exploding gradients, on the other hand, refer to the phenomenon where gradients become excessively large during backpropagation.
When gradients explode, the weight updates become very large, causing the optimization process to become unstable. The optimizer may oscillate around the minimum of the loss function or even overshoot it entirely, preventing the model from converging to a good solution.
Furthermore, extremely large gradient values can lead to numerical overflow, resulting in incorrect computations or the introduction of NaN (Not a Number) values, which can completely derail the training process.
Causes of Exploding Gradients
- Deep Networks: Similar to vanishing gradients, exploding gradients are more likely in deep networks. However, instead of the gradients shrinking, they can grow exponentially when certain conditions are met.
- Large Weights: Large initial weights or poorly chosen initialization methods can cause the gradients to grow as they are propagated backward, making them larger at each layer.
- High Learning Rates: Large learning rates can also exacerbate the problem of exploding gradients. If the gradient updates are too large, they can cause the network to overshoot the optimal parameters, resulting in instability.
Solutions to Exploding Gradients
- Gradient Clipping: One effective technique to mitigate exploding gradients is gradient clipping, where gradients are capped at a maximum value. If a gradient exceeds this threshold, it is scaled back to prevent it from growing too large.
- Weight Regularization: Techniques like L2 regularization (weight decay) can help prevent weights from growing too large, thus reducing the risk of exploding gradients.
- Proper Initialization: Just as with vanishing gradients, proper weight initialization can help prevent gradients from exploding. Using techniques such as Xavier/Glorot or He initialization can prevent excessively large gradients during backpropagation.
- Lower Learning Rates: Using a smaller learning rate can help prevent the gradients from becoming too large in the first place, allowing for more stable updates during training.
Subscribe to our newsletter!